Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 1b
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua.
Passo 1
Temos que é uma reta e seu gráfico é dado por:
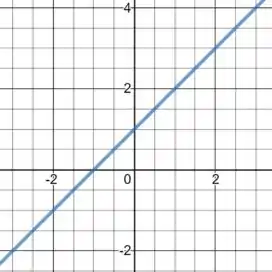
Como nessa reta não temos nenhum salto, então dizemos que ela é contínua em todo o seu domínio que é a reta real.
é contínua para todo .
Resposta
é contínua para todo .
Exercícios de Livros Relacionados
Se a função produto h x =f x . g ( x ) é contínua em x = 0 , f ( x ) eg ( x ) devem ser continuam em x = 0 ? Justifique sua resposta.
É verdade que, se esticarmos um elástico movendo uma ponta para a direita e outra para a esquerda, algum ponto do elástico continuará em sua posição original? Justifique sua resposta.
Seja f definida em um intervalo (a, b) e suponha que f ( c ) ≠ 0 em algum c onde f seja contínua. Mostre que há um intervalo ( c - δ ,c +δ ) em torno de c onde f tem o mesmo sinal que f(c).
Prove que f é continua em c se, e somente se, lim h → 0 f c + h = f c .
Suponha que um função f seja contínua no intervalo fechado [0,1] e que 0 ≤ f x ≤ 1 para qualquer x em [0,1]. Mostre que deve existir um numero c em [0,1], de modo que f c = c . (c é chamado de ponto f