Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 27
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
se ,
se ,
,
,
se
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui eu e você iremos encontrar um gráfico de que se encaixe em todas as condições dadas.
Passo 2
Como se então é crescente para valores de entre e .
Como se então é decrescente para valores de menores que ou maiores que .
Se então possui reta tangente horizontal em
Passo 3
Há uma assíntota vertical em devido ao limite fornecido e não está definida para esse ponto.
Como se então possui concavidade para cima em valores de que não sejam e
Passo 4
Logo, temos o seguinte gráfico:
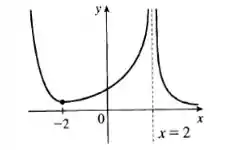
Resposta
Exercícios de Livros Relacionados
Em cada parte, faça um esboço aproximado do gráfico usando assíntotas e limites apropriados, mas não derivadas. Compare seu esboço ao gerado por um recurso gráfico computacional. y = 3 x 2 - 8 x 2 - 4
Em cada parte, faça um esboço aproximado do gráfico usando assíntotas e limites apropriados, mas não derivadas. Compare seu esboço ao gerado por um recurso gráfico computacional. y = 2 x - x 2 x 2 + x
Suponha que f ( x )=P ( x ) / Q ( x ) , em que P e Q são polinômios sem fator comum. Se y=5 for uma assíntota horizontal do gráfico de f , então P e Q terão o mesmo grau.
Se o gráfico de f ' tiver uma assíntota vertical em x = 1 , então f não pode ser contínua em x = 1 .
Esboce a forma geral do gráfico de y = x 1 n e descreva o que acontece com essa forma quando n cresce se(a) n for um inteiro positivo par;(b) n for um inteiro positivo ímpar.