Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 26
Esboce a forma geral do gráfico de e descreva o que acontece com essa forma quando cresce se
(a) for um inteiro positivo par;
(b) for um inteiro positivo ímpar.
Passo 1
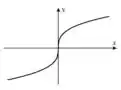
Bom galera, quando é par, a função é definida apenas para ; como aumenta o gráfico se aproxima a linha para .
Assim, graficamente, temos:
Passo 2
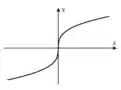
Quando é ímpar, o gráfico é simétrico em relação à origem. Como aumenta o gráfico aproxima a linha para e a linha para .
Portanto, temos
Prontinho!!
Resposta
(a) 
(b) 
Exercícios de Livros Relacionados
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar