Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 28
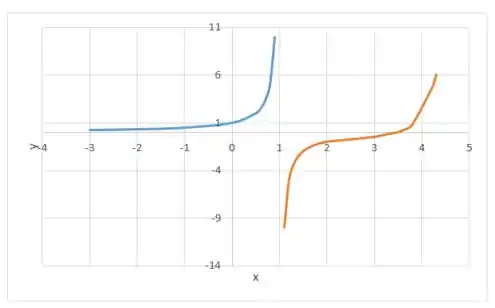
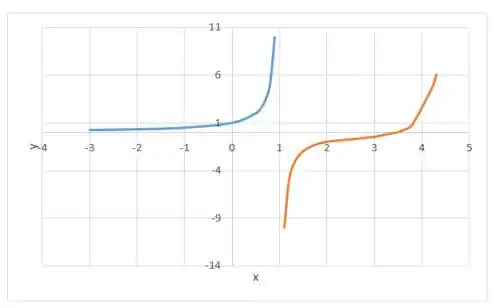
Esboce o gráfico de uma função que satisfaça a todas as condições dadas.
para todo
Assíntota vertical
e ou
se
Passo 1
O enunciado pede pra a gente esboçar um gráfico de uma função desconhecida e nos dá as seguintes informações:
para todo
Assíntota vertical
e ou
se
O que temos nas nossas mãos é um grande quebra cabeça! Antes de qualquer coisa precisamos lembrar que a derivada primeira, indica que a função é crescente e que a função é decrescente.
Já a derivada segunda vai nos falar que a concavidade é pra cima quando ou pra baixo quando !
Então observando as informações acima temos que:
A função é sempre crescente, menos em ;
Se temos uma assíntota vertical em , então aqui vamos dar uma olhadinha em o que precisamos pra ter uma assíntota vertical (vou falar melhor disso no Passo 2);
A concavidade é pra cima nos intervalos e ;
A concavidade é pra baixo no intervalo de ;
Obviamente, com apenas essas informações, vamos ter soluções infinitas! Então é hora de colocar a criatividade pra jogo!
Passo 2
Vamos começar pela assíntota! Para termos uma assíntota vertical precisamos obedecer as seguintes condições:
Ou seja:
Podemos só tentar desenhar alguma curva com essas condições, ou pensar em uma função que se encaixa nesse gráfico. Por exemplo, se não esta definida em podemos ter uma função do tipo:
Assim:
Nesse caso teríamos um gráfico assim:
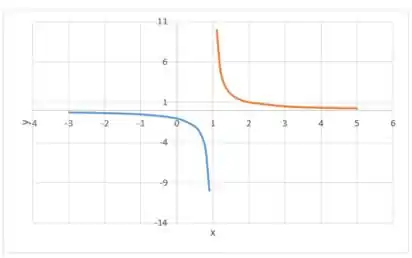
Passo 3
Agora vamos pensar na informação: “A função é sempre crescente, menos em
Isso não quer dizer que a função é decrescente em , quer dizer apenas que a função não esta definida pra . O que faz perfeito sentido com a função que estamos testando!
Mas nem tudo são flores... nossa função teste é decrescente. Pra mudar isso podemos fazer:
Nosso gráfico ficaria:
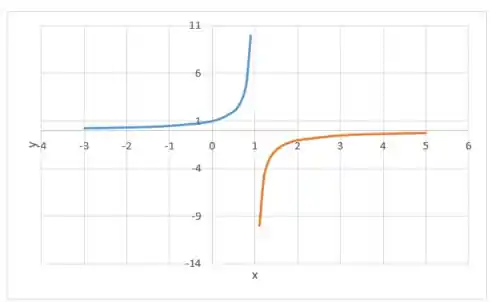
Passo 4
Agora vamos para as informações de concavidade!
A concavidade é pra cima nos intervalos e ;
A concavidade é pra baixo no intervalo de .
Comparando com o gráfico vemos que apenas a parte esquerda esta totamente certa. Então precisamos modificar o gráfico para , sua concavidade deverá ser pra cima e ela deve continuar sendo crescente:
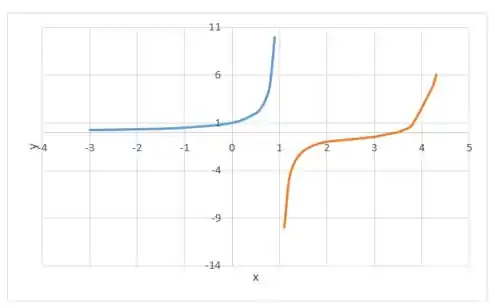
Prontinhooo!
Resposta
