Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 30
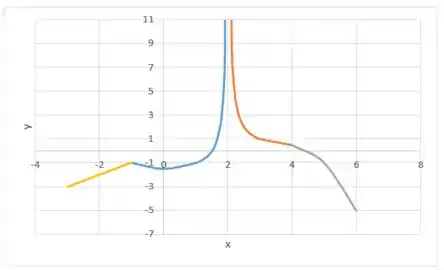
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
, para .
para .
para ou ou .
,
para ou .
para .
Passo 1
O enunciado pede pra a gente esboçar um gráfico de uma função desconhecida e nos da as seguintes informações:
,
para .
para .
para ou ou .
,
para ou .
para .
O que temos nas nossas mãos é um grande quebra cabeça! Antes de qualquer coisa precisamos lembrar que a derivada primeira, indica se a função é crescente ou decrescente. Já a derivada segunda vai nos falar se a concavidade é pra cima ou pra baixo!
Obviamente, com apenas essas informações, vamos ter soluções infinitas! Então é hora de colocar a criatividade pra jogo!
Passo 2
Vamos fazer esse exercício analisando as condições separadamente. Mas não precisa ser na ordem, vamos olhar e tentar pescar qual a condição que nos dá a informação inicial mais interessante!
De cara a gente pode ver:
,
Isso significa que teremos duas assíntotas verticais em . Vamos nos concentrar em uma primeiro e depois vamos pra outra, ok?!
Pensando na primeira assíntota, quando nos aproximamos de pela esquerda. Vamos tentar pescar mais condições onde o intervalo é próximo de , isso pode nos ajudar a ter uma imagem mais rápida:
para
para ou
A nossa função será crescente entre e , o que casa com a informação da assíntota, afinal quando nos aproximamos de pela esquerda vamos para infinito. Além disso entre e temos uma concavidade pra cima. Já podemos começar a rascunhar:
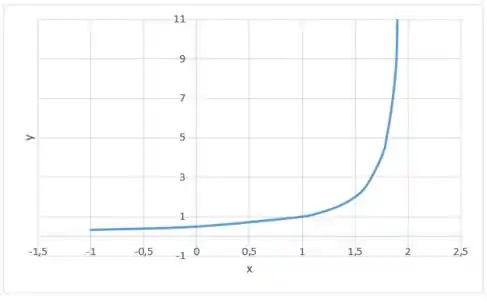
Passo 3
Agora vamos focar na segunda assíntota, olhamos então para as seguintes condições:
para ou ou .
para ou
No intervalo a função será decresce com concavidade pra cima. Assim:
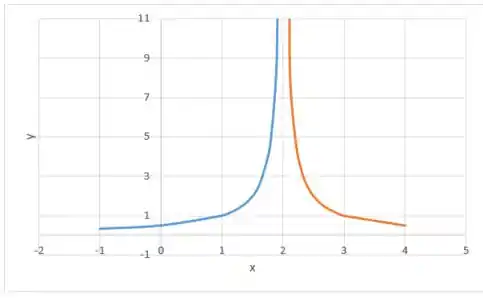
Passo 4
Agora vamos olhar condições onde :
,
para ou ou .
para .
Eem a função será decrescente e em temos:
,
Opa, a derivada é igual a zero. Mas não podemos ter um ponto de máximo ou mínimo, uma vez que antes e depois desse ponto a função é decrescente. Logo temos um ponto de inflexão. Juntando essas informações ao nosso gráfico:
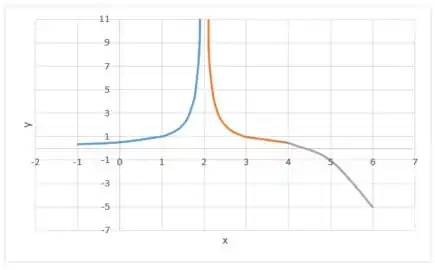
Passo 5
Agora vamos olhar pra :
para .
para ou ou .
para ou .
Entre e temos uma função decrescente com concavidade pra cima, mas isso a gente já aplicou ao gráfico. Podemos ignorar!
Temos uma derivada constante pra . Podemos tirar a seguinte conclusão. Se:
Então:
Afinal, se derivarmos teremos . Aplicando ao nosso gráfico teremos:
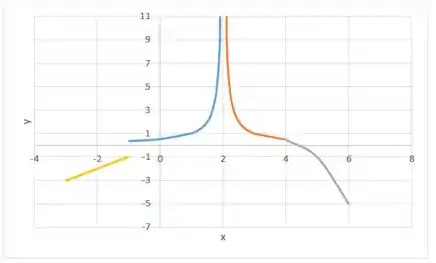
Vamos ajustar esse gráfico pra ficar tudo coladinho:
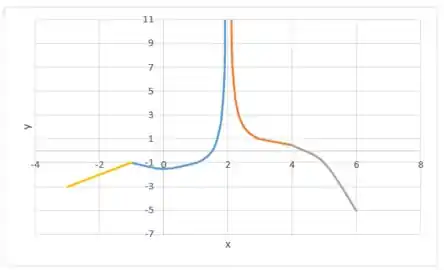
Em temos um mínimo local, conforme as nossas condições!
Resposta
