Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 31
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
se , se , se , tem ponto de inflexão em , , .
Passo 1
Fala aí! como vai?
Nesse problema temos algumas condições de uma função e nosso objetivo é esboçar o gráfico de a partir dessas características.
Nesse exercício temos as seguintes condições:
para , para .
para , possui ponto de inflexão
, .
E para resolver esse problema vamos analisar cada uma dessas condições e discutir como ela influencia no gráfico da função!
Bora começar!
Passo 2
Da primeira condição foi dito que para , ou seja, como a derivada da função está relacionada com a inclinação da função, essa condição diz que a função é crescente em todo o intervalo, com exceção de .
A segunda condição diz que para e isso nos diz que a função possui concavidade voltada para cima no intervalo .
Da terceira condição como para , então a função possui concavidade voltada para baixo no intervalo .
E, conforme foi dito, possui ponto de inflexão em , logo, sabemos que ela muda de concavidade para .
Da quinta condição, dos limites, temos duas assíntotas horizontais para a função, uma quando , que é a reta e outra quando , que é a reta .
A partir dessas características, podemos esboçar o gráfico de como:
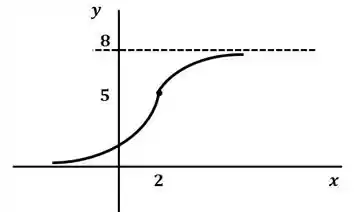
E aí! entendeu tudo? Responde Aí!
Resposta
