Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 30

Faça um gráfico completo de f , indique os limites quando x → ± ∞ e localize todos os extremos relativos, os pontos de inflexão e as assíntotas (quando apropriado).

f x = x 5 - 4 x 4 + 4 x 3

Passo 1

Analisando os limites laterais da função:

lim x → + ∞ ⁡ x 5 - 4 x 4 + 4 x 3 = ∞ 5 = + ∞

lim x → - ∞ ⁡ x 5 - 4 x 4 + 4 x 3 = - ∞ 5 = - ∞

Passo 2

Analisando graficamente não encontramos as assíntotas, e funções polinomiais simples de grau 1 ou mais não podem ter assíntotas.

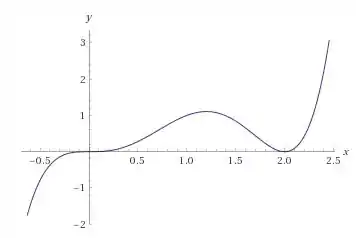
Passo 3

Para encontrar os pontos de inflexão, vamos calcular a primeira derivada da função e encontrar suas raízes. A seguir, aplicamos as raízes na segunda derivada.

Sendo a função :

f x = x 5 - 4 x 4 + 4 x 3

Derivando o polinômio :

f '   x = 5 x 4 - 16 x 3 + 12 x 2

Agora, precisamos encontrar as raízes desse polinômio. Se

f ' x = x 2 ( 5 x 2 - 16 x + 12 )

Uma das raízes do polinômio será x = 0 .

As demais raízes podem ser calculadas se :

( 5 x 2 - 16 x + 12 ) = 0

Aplicando na fórmula de resolução de equações quadráticas:

x = - b ±   b 2 - 4 a c 2 a = - - 16 ±   - 16 2 - 4 . 5 . 12 2 . 5

x ' = 1,2

x ' ' = 2

Passo 4

Agora, podemos calcular a segunda derivada:

f '   x = 5 x 4 - 16 x 3 + 12 x 2

f ' ' x = 20 x 3 - 48 x 2 + 24 x

Aplicando o valor de x = 0 temos que:

f ' ' 0 = 0

f ' ' 1,2 = 20 . 1,2 3 - 48 . 1,2 2 + 24 . 1,2 = - 5,76 < 0   m á x i m o   r e l a t i v o

f ' ' 2 = 20 . 2 3 - 48 . 2 2 + 24 . 2 = 16 > 0     m í n i m o   r e l a t i v o

E afinal, o que são pontos de inflexão? São os zeros da segunda derivada:

f ' ' x = 20 x 3 - 48 x 2 + 24 x = 0

x ( 20 x 2 - 48 x + 24 ) = 0

A primeira raiz x = 0 .

Resolvendo :

x = - b ±   b 2 - 4 a c 2 a = - - 48 ±   - 48 2 - 4 . 20 . 24 2 . 20

x ' = 1 , 689

x ' ' = 0,7101

Resposta

Limite tende a menos infinito pela esquerda e mais infinito pela direita.

Não há assíntotas.

f ' ' 2 > 0 é um ponto de mínimo.

f ' ' 1,2 < 0 é um ponto de máximo.

Pontos de inflexão: x = 0 ;   x ' = 0,7101 e x ' ' = 1,689

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o gráfico da curva y = x 1 3 ( x - 4 )
Faça o gráfico da curva y = x e - x 2
Faça o gráfico da curva y = x 2 ( 2 x 2 - 9 )
Faça o gráfico da curva y = x - 3 2 e x
Se y ' = x 2 ( 6 - 4 x ) Em quais pontos, se houver, o gráfico de f tem um máximo local,um mínimo local ou um ponto de inflexão?Esboce a forma geral do gráfico.