Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 4
Do gráfico de , diga os intervalos em que é contínua.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
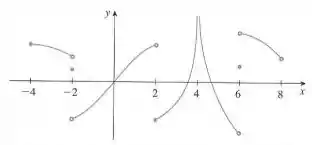
Esta questão cobra visualmente o conceito de continuidade. O enunciado fornece o gráfico de uma função e pede os intervalos em a função é contínua. Notemos que o gráfico não está definido para e , de modo que nossa análise se restringe ao intervalo .
Vale lembrar que, intuitivamente, uma função é contínua em um determinado intervalo o seu gráfico não apresentar saltos ou buracos.
Passo 2
No intervalo entre e o gráfico de não apresenta saltos nem buracos, de modo que nesse intervalo ela é contínua.
Todavia, em ela não é contínua (salto), de modo que o intervalo deve ser dado na forma já que o não deve ser incluído no intervalo.
Passo 3
O mesmo vale para o intervalo já que também não está incluído e ir para pela esquerda e pela direita dão valores diferentes.
Nos intervalos e , também é contínua.
A função não está definida em e o gráfico de se aproxima da reta vertical tanto pela direita quanto pela esquerda, porém nunca a intersecta. Dizemos então que a reta é uma assínta vertical.
Por fim, no intervalo a função também é contínua.
Resposta
Os intervalos são: , , , e