Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 3
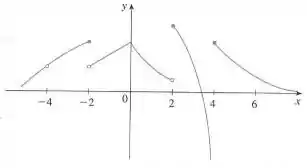
a) Do gráfico de , explique os pontos em que é descontínua e explique por quê.
b) Para cada um dos pontos indicados na parte (a), determine se é contínua à direita, à esquerda ou nenhum deles.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
A questão cobra de forma visual o conceito de continuidade. O enunciado nos fornece o gráfico de uma função e pede, no item (a), para procurarmos os pontos em que não é contínua. No item (b) é pedido para verificar se existem pontos de continuidade lateral. É importante lembrar que uma função é contínua lateralmente em um ponto se um dos limites laterais de for igual ao valor da função naquele ponto.
Para que o limite da função seja continua, devemos ter:
Isso é, o limite da função e a imagem da função deve ser o mesmo no ponto dado.
Mas na prática, se a gente pensar em desenhar essa curva no papel, os pontos de descontinuidade vão ser quando a gente tira o lápis do papel.
Passo 2
(a) Uma função contínua não tem buracos, saltos ou quinas. Notemos que a função tem um buraco em , o que significa que ela não está definida neste ponto, e saltos em , e , que significa que seus limites laterais serão diferentes, e consequentemente o limite não existirá. Assim, não é contínua nesses pontos.
Passo 3
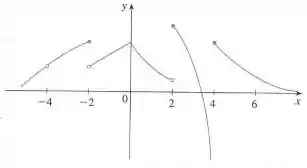
(b) Como é um ponto em que o gráfico de tem um buraco, significando que não está definida neste ponto, a função não é contínua nem à direita nem à esquerda neste ponto.
Em , é contínua à esquerda pois o limite lateral à esquerda é igual ao valor da função, isto é,
Em , é contínua à direita pois o limite lateral à direita é igual ao valor da função, isto é,
O mesmo ocorre em : a função é contínua à direita.
Resposta
a) , , e .
b) Contínua à direita: e .
Contínua à esquerda: .
Nenhuma delas: .