Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.5 - Ex. 15
Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Falaaa... tudo bem??
Nessa questão vamos explicar por que a função:
É descontínua no ponto:
Pra isso vamos lembrar que pra uma função ser contínua ela tem que satisfazer três coisinhas:
1. está definida (ou seja, deve estar no domínio de )
2. deve existir (aqui verificamos se os limites laterais são iguais)
3. (o limite naquele ponto deve ser igual à função naquele ponto)
Vale lembrar também que funções logarítmicas têm restrição. O que está dentro do log deve ser sempre maior que zero.
Passo 2
Vamos identificar o domínio de .
Como temos uma função logarítmica (ln é log na base , lembra?), então o que está dentro do ln deve ser maior que zero:
Pooo... sei que quando tem módulo é meio assustador, mas nessa questão nem vamos precisar analisar o módulo. Só vamos precisar lembrar que quando tem módulo, isso vai ser sempre positivo ou igual a zero.
Hummmm... mas pela condição de cima não podemos ter, dentro do log, nada igual a zero, né? Então o valor de que tornar o módulo igual a zero não vai estar no domínio.
Vamos achar que valor de é esse:
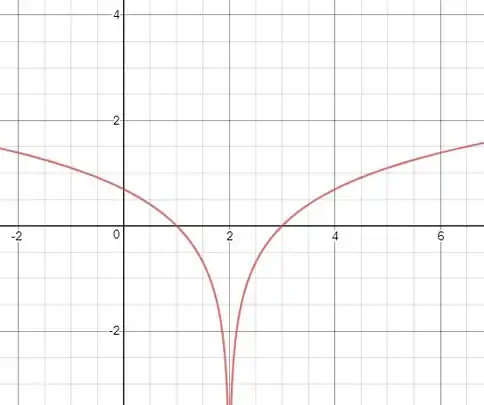
Então o único valor que não está no domínio da função é o .
Ou seja, a função não está definida em . Que já não satisfaz a nossa primeira condição, né?
Como a função não está definida em , então ela não é contínua neste ponto.
Passo 3
Pra ajudar no esboço do gráfico, podemos destrinchar um pouco o módulo lembrando que quando temos módulo, podemos separar em duas partes. A gente achou o valor que zera a expressão de dentro do módulo, certo? Então pra valores abaixo desse valor, nós usamos a expressão de dentro do log multiplicada por -1, e para valores acima fica tudo igual:
Então no gráfico vamos ter o formato de quando for menor que e o formato de quando for maior que :
Resposta
R: demonstração e esboço de gráfico.