Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 14
- Esboce o gráfico de uma função que tenha dois máximos locais e um mínimo local, mas nenhum mínimo absoluto.
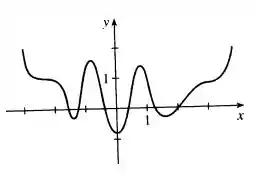
- Esboce o gráfico de uma função que tenha três mínimos locais, dois máximos locais e sete números críticos
Passo 1
Fala, falaNessa questão queremos encontrar possíveis gráficos dadas algumas condições.
a)
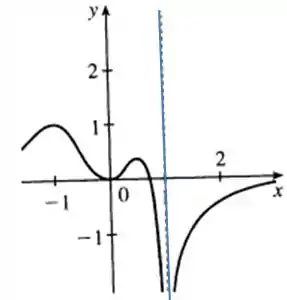
função que tenha dois máximos locais, um mínimo local, mas nenhum mínimo absoluto.
Como a função não possui um mínimo absoluto, podemos concluir que ela forma uma assíntota vertical, ou então que ela vá decrescendo infinitamente, então, esboçando uma função qualquer com assíntota vertical.
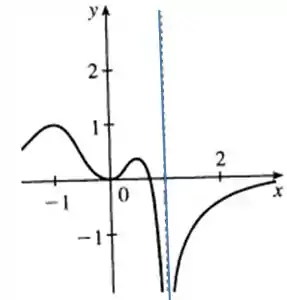
Ela também vai precisar ter dois máximos locais, ou seja duas concavidades para baixo.
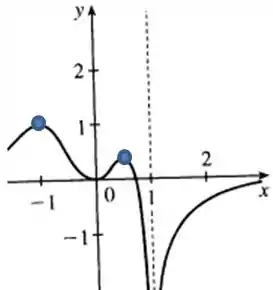
E ela também tem um mínimo local, ou seja, uma concavidade para cima.
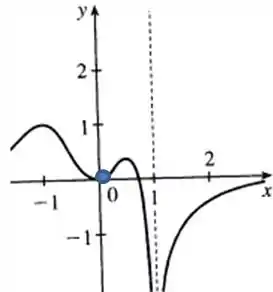
Passo 2
Na b) queremos uma função tenha 3 mínimos locais, dois máximos locais e 7 números críticos.
Um número crítico é quando a derivada da função é igual a zero.Isso ocorre nos mínimos e máximos locais.
Portanto, como temos 5 desses, faltam ainda outros dois pontos que possuem derivada zero, mas que não são de máximo ou mínimo local.
Esses pontos serão pontos de inflexão.
Vou primeiro colocar os máximos e mínimos locais.
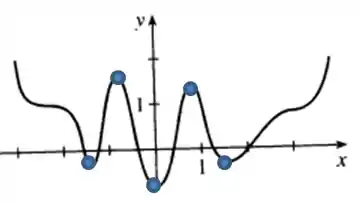
E agora os pontos de inflexão (onde a concavidade muda de direção).
Perceba que em todos pontos marcados, a função possui derivada igual a zero. Mas nos pontos em x a função troca de concavidade e nos pontos com bolinha a função tem máximo ou mínimo local.
Resposta
a)
b)
