Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 46
Dê um zoom em direção aos pontos e sobre o gráfico da função . O que você observa? Explique o que você viu em termos da diferenciabilidade de .
Passo 1
E aí, tudo bem?! Temos a função:
Aqui a gente precisa plotar esse gráfico e depois dar um zoom em direção as pontos e . Depois temos que analisar esses pontos, compara-los e no final dar o nosso veredito sobre a diferenciabilidade de !
Aqui a gente não precisa esboçar na mão! No livro tem uma figurinha rosinha do lado desse enunciado. Isso significa que ele espera que você plote o gráfico com o auxílio de um software, que pode ser um programa ou um site!
Pra uma função ser diferenciável em um ponto deve ser contínua nesse ponto, mas quando a curva tem uma mudança abrupta, como uma “quina” ou uma “dobra” , ou então um ponto de inflexão, ela não vai ser derivável!
Agora vamos ao que interessa, mãos à obra!
Passo 2
Plotando o gráfico:
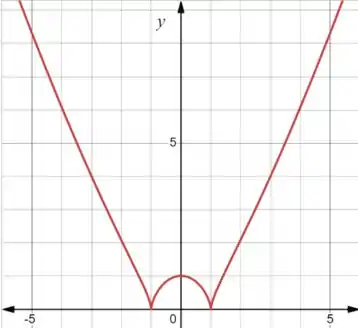
Agora o zoom nos pontos e :
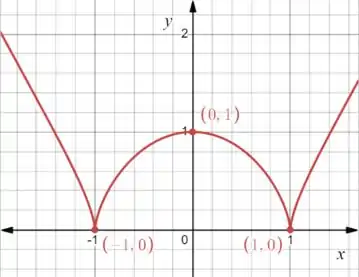
A gente pode observar que para a função é decrescente. Em ela passa a ser crescente, passa por um ponto de máximo em , volta a ser decrescente e em passa a ser crescente de novo!
Muitas mudanças de inclinação! Mas repara que em essa mudança acontece de uma forma suave, poderíamos passar uma reta tangente nesse ponto e ela seria horizontal. Certo?!
Só que em e isso acontece de forma abrupta e se passássemos uma reta tangente nesses pontos teríamos tangentes horizontais.
E qual é a inclinação de uma reta vertical?!
Seria infinito, certo?! Se não é um número então dizemos que a função não é diferenciável nesses pontos!
Beleza, mas esses são os únicos pontos “problemáticos�� da função, certo?!
Então, podemos dizer que a função é derivável, exceto nos pontos e !
Resposta
Esboço do gráfico e desenvolvimento.