Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 15

Esboce o gráfico do integrando e use áreas para calcular a integral

∫ - 2 4 x 2 + 3   d x

Passo 1

A integral da nossa questão será resolvida através da associação com a área entre a nossa curva e o eixo X. Precisamos então esclarecer alguns pontos para que possamos resolvê-la. Eles são: os limites do eixo X e qual o comportamento da nossa função neste intervalo.

Passo 2

Vamos começar por determinar o intervalo de análise. O intervalo será dado por [ a , b ] , em que a é o limite inferior da nossa integral e b o limite superior. Desta forma, temos:

a = - 2

b = 4

Passo 3

Vamos obter agora o gráfico da nossa função. Portanto, temos:

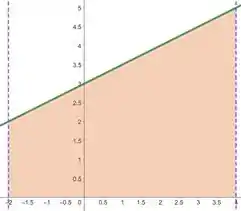
Em destaque temos a área da região que devemos calcular, à qual possui a forma de um trapézio retangular.

Passo 4

A área de um trapézio é:

A = B a s e m a i o r + B a s e m e n o r ⋅ h 2

A altura do nosso trapézio é o comprimento do intervalo de integração. Isto é:

h = 4 - - 2 = 6

Já as bases maior e menor é a interseção de f x = x 2 + 3 com as retas x = 4 e x = - 2 , respectivamente. Portanto, obtemos os seguintes valores:

B a s e m a i o r = 4 2 + 3 = 5

B a s e m e n o r = - 2 2 + 3 = 2

Calculando a área, temos:

A = 5 + 2 ⋅ 6 2 = 21

Logo,

∫ - 2 4 x 4 + 3   d x = 21

Resposta

∫ - 2 4 x 4 + 3   d x = 21

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dê o valor aproximado da integral definida , usando uma calculadora para determinar, até 4 casas decimais a soma de Riemann correspondente , com partições regulares n , sendo a soma feita à esquerda o
Dê o valor aproximado da integral definida , usando uma calculadora para determinar, até 4 casas decimais a soma de Riemann correspondente , com partições regulares n , sendo a soma feita à esquerda o
Expresse a medida da área exata da região pelo Limite da Soma de Riemann e Integral . E depois, Calcule essa área.Limitada pela reta y = x³-4 , pelo eixo x e pelas retas x = -2 e x = -1
Expresse a medida da área exata da região pelo Limite da Soma de Riemann e Integral . E depois, Calcule essa área.Limitada pela reta y = 4 - x² , pelo eixo x e pelas retas x = 2 e x = 1
Expresse a medida da área exata da região pelo Limite da Soma de Riemann e Integral . E depois, Calcule essa área.Limitada pela reta y = 12 - x – x² , pelo eixo x e pelas retas x = 2 e x = -3