Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 24
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de . (Use os gráficos e as transformações das Seções 1.2 e 1.3.)
Passo 1
Fala galera.. Nessa questão temos que esboçar o gráfico da função
E a partir dele encontrar os valores máximos e mínimos locais e absolutos da função.
Passo 2
A função módulo de é uma função cujo gráfico conhecemos, ele forma um V.
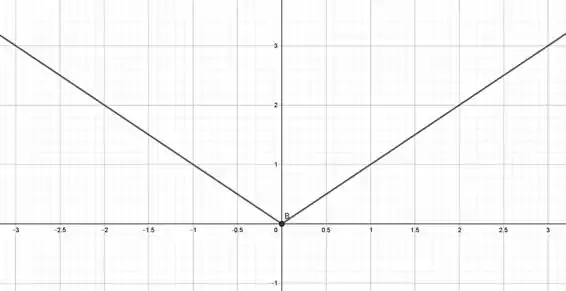
A partir dele, vamos verificar se essa função possui máximo e mínimo locais ou absolutos.
Passo 3
Nesse caso não temos pontos máximos nem mínimos locais. Só o ponto que é mínimo absoluto.
- Pontos de máximo locais: não tem. Você pode perceber que não há um ponto onde a função cresce e depois passa a decrescer.
- Ponto máximo absoluto: não tem (a função cresce indefinidamente)
- Pontos de mínimo locais: não tem. Você pode perceber que não há um ponto onde a função decresce e depois passa a crescer, além é claro, do mínimo absoluto.
- Ponto mínimo absoluto:
Resposta
Somente ponto mínimo absoluto:
Exercícios de Livros Relacionados
33-36 Encontre os extremos relativos usando os testes da derivada primeira e da derivada segunda.36. f x = x - 3 e x
37-50 Use qualquer método para encontrar os extremos da função f .37- f x = x 4 - 4 x 3 + 4 x 2
25-32 Use a derivada dada para encontrar todos os pontos críticos de f e, em cada um deles, determine se ocorre um máximo relativo, um mínimo relativo ou nenhum desses. Suponha, em cada caso, que f se
25-32 Use a derivada dada para encontrar todos os pontos críticos de f e, em cada um deles, determine se ocorre um máximo relativo, um mínimo relativo ou nenhum desses. Suponha, em cada caso, que f se
25-32 Use a derivada dada para encontrar todos os pontos críticos de f e, em cada um deles, determine se ocorre um máximo relativo, um mínimo relativo ou nenhum desses. Suponha, em cada caso, que f se