Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 11
Faça o gráfico da função.
Use a regra de L’Hôspital para explicar o comportamento quando .
Estime o valor mínimo e os intervalos de concavidade. Então, use o cálculo para achar os valores exatos.
Passo 1
Bom galera, nesse exercício estamos interessados em esboçar o gráfico da função
para ver o comportamento da função e estimar o valor de mínimo e intervalo de concavidade.
Aqui vamos usar uma ferramenta gráfica para esboçar o gráfico de .
A questão também pede para usarmos a regra de L’hospital para avaliar o comportamento de quando , ou seja:
A regra de L’hospital nos diz que quando temos uma indeterminação do tipo ou , basta derivarmos o numerador e o denominador até que a indeterminação suma.
Nesse caso, nossa função não é uma fração, portanto, precisamos transforma-la em uma fração para poder aplicar a regra de L’hospital.
Para o cálculo, vamos usar que o ponto de mínimo ocorre quando
E a derivada troca de negativa para positiva nesse ponto.
Para os intervalos de concavidade, vamos usar a segunda derivada da função e avaliar que quando
A função é côncava para cima e quando
A função é côncava para baixo.
Após estimar graficamente, iremos conferir nossa resposta utilizando o cálculo para achar o valor exato.
Passo 2
Fazendo o gráfico da função
Temos o seguinte:
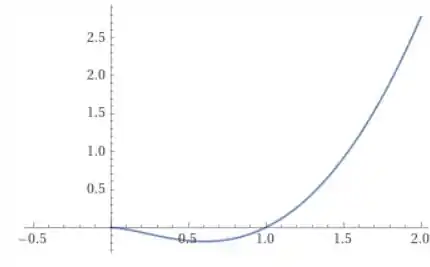
Podemos perceber que essa função não é definida para valores negativos de , o que faz sentido, pois o logaritmo natural precisa ter um argumento positivo maior que zero.
Também podemos perceber que a função possui um ponto de mínimo próximo de .
Passo 3
Vamos utilizar a regra de L’Hôspital para estimar o valor da função quando .
Como a função não é definida para valores negativos, não faz sentido olharmos para ela tendendo a zero por valores de menores que zero. Isso é,
Ou seja, essa função só irá possuir limite pela direita quando tende a zero.
Se substituirmos esse limite, obtemos:
Que é uma indeterminaç��o. Para transforma-la numa indeterminação onde possamos usar L’hospital, devemos transformar essa função numa fração:
Utilizando a regra, temos
Substituindo o limite temos:
O que é condizente com o gráfico que obtemos no Passo 2.
Passo 4
Agora devemos encontrar o ponto de mínimo e o ponto de inflexão.
O ponto de mínimo que está no gráfico podemos encontrar derivando uma vez e igualando a zero.
Nossa função é
Sua derivada é, pela regra do produto:
Igualando a zero temos:
Portanto,
Esse é o ponto de mínimo que encontramos no gráfico.
Derivando novamente encontramos:
A função é côncava para cima quando , então
Dessa forma, possui concavidade para cima em e concavidade para baixo em .
O ponto de inflexão é
Resposta
cresce em e decresce em . Podemos ver também que é um valor de mínimo local e é o ponto . Possui concavidade para cima em e concavidade para baixo em . O ponto de inflexão é .