Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.6 - Ex. 3
Faça gráficos de que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de e para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.
Passo 1
Oi, pessoal! Vamos resolver essa questão?
O enunciado nos dá a função
e pede para estimarmos alguns aspectos importantes da curva dessa função: onde ela cresce, onde ela decresce, os picos e os vales (valores extremos), onde ela se curva pra cima, pra baixo, e onde ela muda de curvatura.
Dessa forma, precisamos utilizar os gráficos de e para encontrar as estimativas para:
- Os intervalos de crescimento e decrescimento.
- Os valores extremos.
- Os intervalos de concavidade.
- Os pontos de inflexão.
🤔 Mas porque será que precisamos dos gráficos das derivadas de para isso? Então, é o seguinte:
- Os intervalos onde a função cresce e decresce são determinados pelos sinais da primeira derivada
- Os pontos onde a função atinge máximos e mínimos são raízes de
- Os intervalos de concavidade são determinados pelos sinais da segunda derivada
- Os pontos de inflexão, onde a curva muda de concavidade, são raízes de
O que precisamos fazer para resolver a questão é:
- Encontrar as funções e e obter os seus gráficos, assim como o gráfico da função
- Estimar os pontos críticos, valores extremos e os intervalos de decrescimento e crescimento usando os gráficos de e de
- Estimar os pontos de inflexão e os intervalos de concavidade usando os gráficos de e de
Não vamos dar tanta atenção para a construção do gráfico de , combinado? Nosso objetivo é usá-los, junto com conceitos de cálculo, para estimar algumas características importantes da função .
Você pode utilizar calculadoras gráficas para a obtenção dos gráficos 🙌!
Bora colocar a mão na massa?
Passo 2
Bem, como a função é um polinômio, vamos derivá-la utilizando a Regra da Soma e, para cada um dos seus termos, vamos utilizar a Regra da Potência.
Relembrando a Regra da Potência:
Dessa forma, a primeira derivada é dada por
Realizando o mesmo processo para , temos que a segunda derivada é dada por
Passo 3
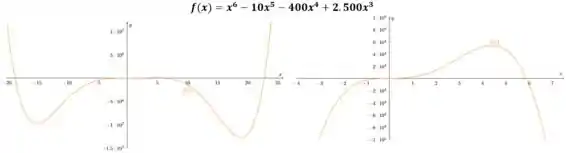
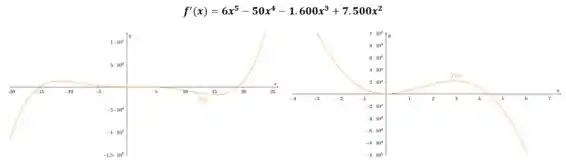
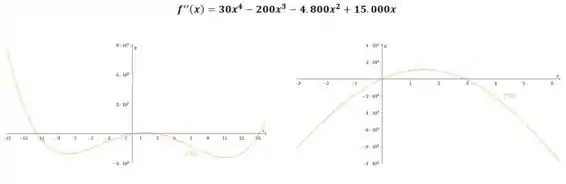
Neste passo, vamos apenas plotar os gráficos de e
Para cada uma das funções, plotamos gráficos considerando duas escalas distintas, pois assim vamos conseguir entender melhor alguns comportamentos das curvas.
⚠️Fique atento quando fizer os seus gráficos!
Como o domínio da função não foi dado, talvez você precise escolher intervalos de e (janelas) mais adequados para conseguir visualizar melhor algumas características das curvas.
Passo 4
Com base no gráfico de , podemos estimar os pontos críticos, valores extremos e os intervalos de decrescimento e crescimento.
Quer ver como?
- Os pontos onde aparenta ser zero são aproximadamente:
- Olhando para o gráfico de, vemos que
- é um mínimo local.
- é um ponto de inflexão (não é máximo nem mínimo local).
- é um máximo local.
- é um mínimo global.
- Olhando para o gráfico de , percebemos que nos intervalos e a função é positiva. Logo, nesses intervalos a função é crescente, como pode ser visto no seu gráfico.
- Olhando para o gráfico de , no intervalo intervalos e a função é negativa. Logo, nesses intervalos a função é decrescente, como pode ser visto no seu gráfico.
- Os pontos onde aparenta ser zero são aproximadamente:
e .
Esses são os pontos críticos da função
Passo 5
Com base no gráfico de , podemos estimar os pontos de inflexão e os intervalos de concavidade.
Vamos lá!
e .
Esses são candidatos a pontos de inflexão da função
- Olhando para o gráfico de , percebemos que nos intervalos , e a função é positiva. Logo, nesse intervalo a concavidade de é voltada para cima, conforme pode ser visto no seu gráfico.
- Olhando para o gráfico de , percebemos que nos intervalos e a função é negativa. Logo, nesse intervalo a concavidade de é voltada para baixo, conforme pode ser visto no seu gráfico.
- Como nos pontos
e ,
a segunda derivada muda de sinal, então todos são pontos de inflexão da função , como pode ser visto no gráfico de .
Resposta
As respostas foram dadas nos passos anteriores.