Obtenha gráficos de que revelem todos os aspectos importantes da curva. Em particular você deve usar os gráficos de e para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.
Passo 1
Bom galera, nesse exercício queremos tirar conclusões e estimar propriedades importantes das funções com base em um gráfico previamente feito.
Nós temos a função que é dada por
Definida para .
Vamos usar então um software gráfico para plotar essa função e também as suas derivadas primeira e segunda .
As principais propriedades que queremos estimar são os intervalos de crescimento e decrescimento , valores extremos, intervalos de concavidade e pontos de inflexão.
Da teoria, temos que a função cresce quando sua derivada é positiva
E a função decresce quando sua derivada é negativa
Valores extremos são os máximos e mínimos da função. Temos que eles vão ocorrer quando a primeira derivada trocar de sinal, o que geralmente ocorre quando
Um ponto de máximo vai ocorrer quando a derivada passa de positiva para negativa, o que indica que a função crescia, chegou no máximo e então passa a decrescer.
Um ponto de mínimo ocorre quando a derivada passa de negativa para positiva.
Com relação a concavidade e pontos de inflexão, estes estão atrelados a segunda derivada .
A função é côncava para cima quando a segunda derivada é positiva
E a função é côncava para baixo quando a segunda derivada é negativa
Os pontos de inflexão ocorrem quando a segunda derivada troca de sinal, o que geralmente ocorre em
Bora lá então?!
Passo 2
Bom galera, primeiramente iremos encontrar a primeira e a segunda derivada da nossa função para assim fazer o gráfico da função e das suas derivadas.
Nossa função é:
Derivando , temos
Derivando , temos
Passo 3
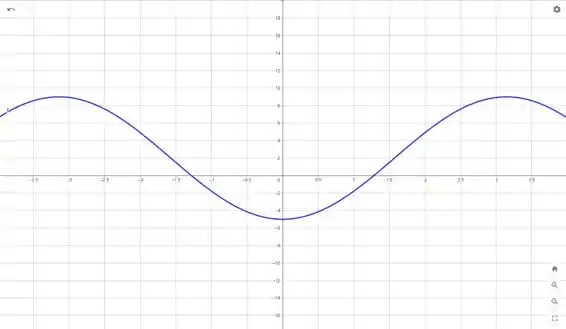
Podemos então gerar os seguintes gráficos
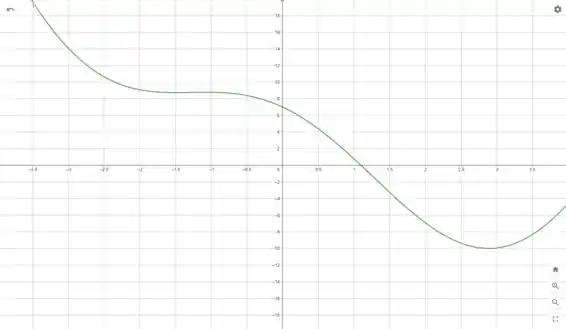
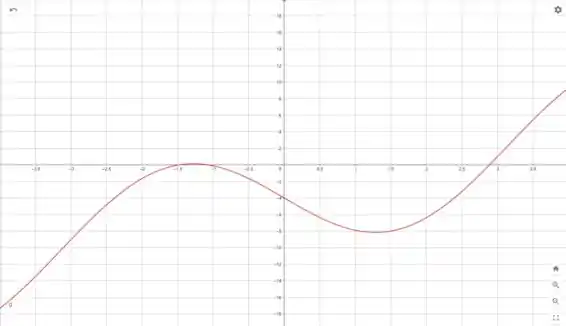
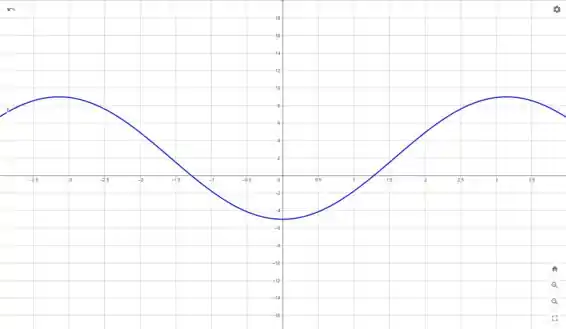
Com base no gráfico de , podemos encontrar o intervalo de decrescimento e crescimento. Para isso, devemos ver onde o gráfico de é menor que zero.
Assim, o intervalo de decrescimento é
e o intervalo de crescimento é
Podemos ver também os valores de máximo e mínimo, que ocorrem quando .
São valores de máximo os pontos
Pois antes dele a função crescia e depois dele a função decresce .
São valores de mínimo os pontos
Pois antes deles a função decrescia e depois deles a função cresce .
Com base no gráfico de , podemos estimar os intervalos de concavidade. Para isso, devemos ver onde o gráfico de é maior que zero, que é onde a concavidade é para cima.
Assim, a nossa função possui concavidade para cima em
e concavidade para baixo em
E os pontos de inflexão ocorrem quando a segunda derivada vale zero e troca de sinal. Portanto, são pontos de inflexão:
Pronto!
Resposta
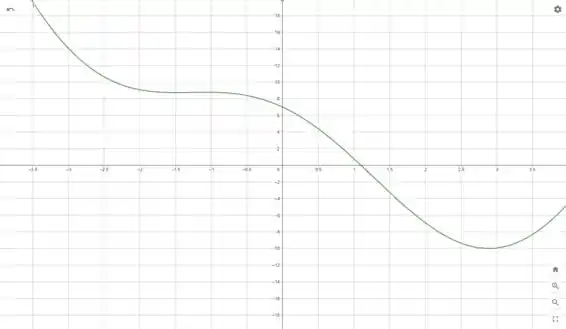
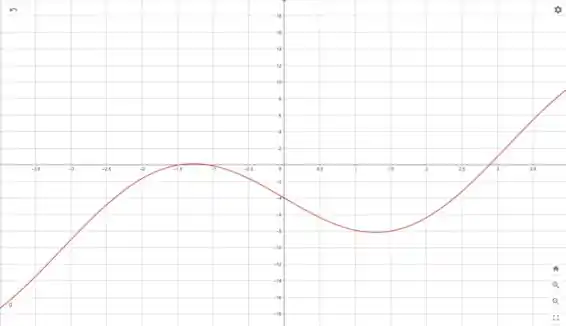
O intervalo de decrescimento é
e o intervalo de crescimento é
São valores de máximo os pontos
São valores de mínimo os pontos
A função possui concavidade para cima em
e concavidade para baixo em
São pontos de inflexão: