Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.6 - Ex. 8
Obtenha gráficos de que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de e para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.
Passo 1
Fala aí... tudo de boas?
Nessa questão temos a seguinte função
E o enunciado pede pra gente usar os gráficos de e para obter aspectos importantes sobre a curva .
O gráfico da derivada primeira vai nos dar informações acerca do crescimento e decrescimento da função, pois se
A função cresce e se
A função decresce.
Além disso, um ponto onde a derivada troca de sinal indica que a função possui um valor extremo.
Se a função crescia e passa a decrescer, então temos ali um ponto de máximo local. Se a função decrescia e passa a cresce, então temos ali um ponto de mínimo local.
Já o gráfico da segunda derivada vai nos dar informações acerca da concavidade da função, pois se
A função é côncava para cima e se
A função é côncava para baixo.
Da mesma forma, um ponto onde a derivada segunda troca de sinal indica que a função possui um ponto de inflexão, isso é, um ponto onde ela troca de concavidade.
Passo 2
Vamos começar encontrando a nossa derivada primeira.
A função dada é:
Usando a regra do quociente para derivadas, temos que:
Vamos fazer um estudo de sinais para essa derivada.
Temos que é sempre positiva.
é sempre positiva por estar sendo elevada ao quadrado.
Por fim temos
Aplicando Bhaskara vemos que suas raízes são
E
Como para essa fator de segundo grau, temos que ele possui concavidade para cima e portanto, ele é negativo quando
E positivo quando
Dessa forma, a função decresce quando está no intervalo e cresce quando está no intervalo .
São pontos críticos os valores e .
Como a função cresce antes de e depois decresce, temos que é um ponto de máximo.
Como a função decresce antes de e depois cresce, temos que é um ponto de mínimo.
Passo 3
Agora, encontrando a derivada segunda da nossa função, temos que derivar a primeira derivada.
Aplicando a regra do produto e a regra do quociente temos:
Ajeitando isso, chegamos em:
Essa segunda derivada aí é meio complicada de encontrar seu estudo de sinal.
Sendo assim, vamos plotar só o seu gráfico e tirar as informações a partir dele.
Passo 4
Usando um software gráfico, vamos plotar o gráfico da primeira derivada que é:
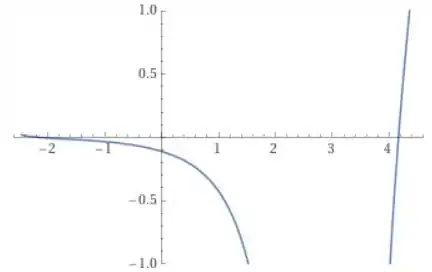
E da segunda derivada que é:
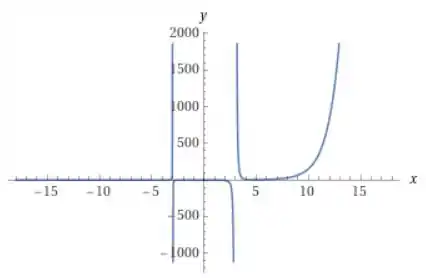
A partir do gráfico da segunda derivada (dando um pouco de zoom), é possível ver que quando está no intervalo e no intervalo .
E a segunda derivada é negativa, isso é, , quando está no intervalo .
Dessa forma, a função é côncava para cima quando está no intervalo e a função é côncava para baixo quando está no intervalo .
Não há pontos de inflexão, porque não tem nenhum local em que a função troca o sinal da derivada, essa troca está sempre separada por assíntotas, que são os pontos e , onde a função original não está definida.
Passo 5
Por fim, vamos plotar o gráfico da função original, para ver se faz sentido o que encontramos.
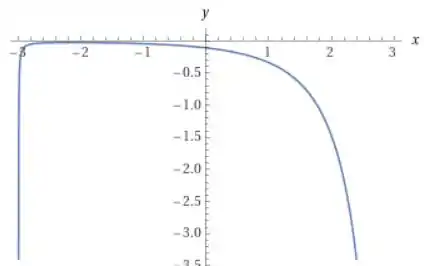
E com uma janela gráfico um pouco maior temos:
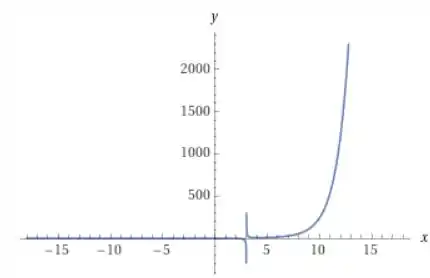
(O software gráfico usado (wolframalpha) teve problemas para plotar a curva com fidelidade. Os pontos e são assíntotas verticais, uma vez que o valor da função vai para infinito e menos infinito nesses pontos. Por algum motivo, o software não conseguiu plotar essas assíntotas.)
Usando o serviço de plotagem de gráficos do google, temos uma resposta melhor:
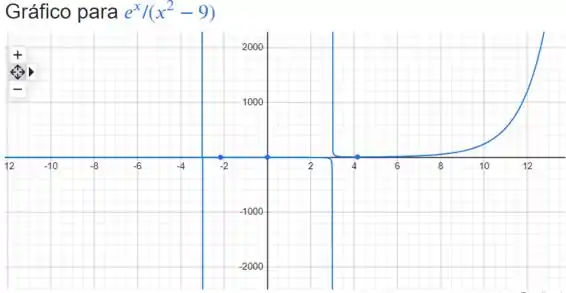
Aqui vemos as concavidades para cima no intervalo e para baixo no intervalo . Os pontos em azul são os pontos de máximo e mínimo local. E o ponto e azul no centro é a interseção com o eixo .
Resposta
Desenvolvimento nos Passos.