Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.1 - Ex. 15
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pede pra gente esbocçar o gráfico de
à mão e usar seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
E para isso podemos fazer uma tabelinha como alguns valores de e calcular o valor da função nesses pontos.
Assim, a mão teremos uma ideia do comportamente da função.
Vemo comigo que te mostro como.
Passo 2
Queremos esboçar o gráfico da função
para .
Para isso vamos começar fazendo uma tabelinha e calculando o valor da função para alguns valores de . Assim:
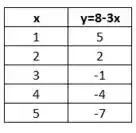
Agora vamos marcar esses pontos em um gráfico. Ficando com:
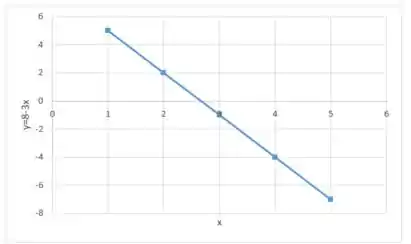
Passo 3
Agora vamos usar esse gráfico para encontrar os valores de máximos e mínimos locais e absolutos de .
Pelo gráfico, podemos ver que não temos valores de máximos e mínimos locais, já que não há picos ou vales em nossa função. Assim,
- Maximo local: Nenhum
- Mínimo local: Nenhum
- Máximo absoluto: .
- Mínimo absoluto: Nenhum
Além disso, observando o extremo do nosso intervalo podemos dizer que:
Já que é de onde o intervalo começa. e
Já que nosso intervalo não possui extremo superior.
E prontinho, análises feitas.
Resposta
Máximo absoluto: .