Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.6 - Ex. 65
Esboce os gráficos de , e em um sistema de coordenadas, onde é uma função qualquer satisfazendo a desigualdade:
Para todo no intervalo . O que você pode dizer sobre o limite de quando ? Explique seu raciocínio.
Passo 1
Então galera, se esboçarmos os gráficos de , e , teremos o seguinte:
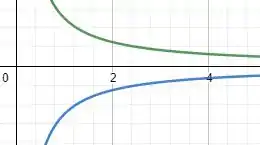
No qual a função em verde é e a função em azul é . Aqui vale ressaltar que a função é uma função que está entre essas duas funções, ou seja, no meio delas! Ok, a primeira parte foi feita!
Passo 2
Para todo no intervalo temos que o limite de para será:
Mas daonde saiu esse resultado? Então galera, utilizando o conceito do Teorema do Confronto e observando com cuidado o gráfico, fica bem tranquilo notarmos que as funções estão tendendo a quando na medida em que aumenta, não é mesmo? Sendo assim, como é uma função que está sendo “esmagada” pelas outras duas (uma superior e outra inferior), então ela terá o mesmo comportamento que as outras! Por isso nosso resultado faz sentido.
Resposta
Ei, a resposta está no passo a passo :)