Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 13

Esboce a região cuja área com sinal é representada pela integral definida e calcule a integral usando uma fórmula apropriada de Geometria quando for necessário.

a )   ∫ 0 3 x   d x c )   ∫ - 1 4 x   d x

b )   ∫ - 1 - 2 x   d x   d )   ∫ - 5 5 x   d x

Passo 1

Vamos esboçar cada uma...

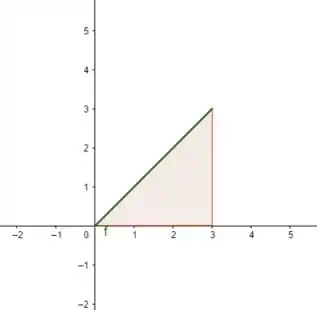
  1. Nessa primeira formou um triângulo, então é só a gente calcular a área do triângulo de base 3 e altura 3 :

    ∫ 0 3 x   d x = 1 2 3 3 = 9 2

    Passo 2

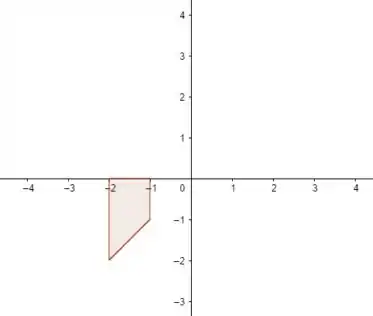
  2. Agora a gente tem um trapézio. Bora calcular a área dele então, lembrando que aqui é pra baixo do eixo, então a área líquida é negativa!

    - A = ∫ - 1 - 2 x   d x = - 2 + 1 ⋅ 1 2 = - 3 2

    Passo 3

  3. Vamos pra terceira agora:

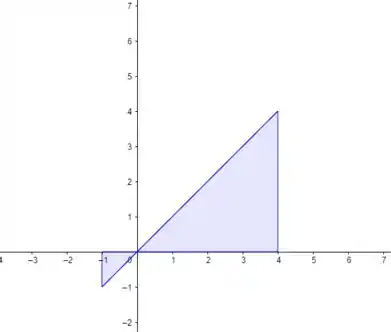
    4. Aqui a gente tem dois triângulos. Vamos calcular a área de cada um e lembrar que esse que tá na parte negativa, a gente vai diminuir do outro...

    ∫ - 1 4 x   d x = A 1 - A 2

    = 4 ⋅ 4 2 - 1 ⋅ 1 2

    = 8 - 1 2 = 15 2

    Passo 4

  4. Vamos ver essa última agora:

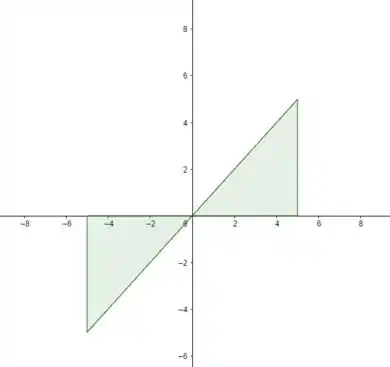
Nesse a gente tem dois triângulos, pra calcular a área líquida, a gente precisa fazer a diferença entre a área positiva e a área negativa. Bora lá então!

∫ - 5 5 x   d x = A 1 - A 2

= 5 ⋅ 5 2 - 5 ⋅ 5 2

= 0

Resposta

  1. 9 2
  2. - 3 2
  3. 15 2
  4. 0
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o centroide da região.A região delimitada pelos gráficos de y = x 2 e y = x + 2 .
Encontre o centroide da região.
Encontre o centroide da região.O triângulo de vértices ( 0,0 ) , ( 1,1 ) e ( 2 , 0 ) .
43. Pode-se mostrar que todo intervalo contém números racionais e irracionais. Aceitando isso, a função. f x = 1s exr a c i o n a l 0s exf o ri r r a c i o n a l Pode ser integrável em um intervalo fe
37-38 Calcule as integrais completando o quadrado e aplicando as fórmulas apropriadas de geometria.38. ∫ 0 3 6 x - x 2 d x