Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 38

A primeira coisa que iremos fazer é olharmos para a expressão dentro da integral, que é essa aqui:

E vamos lembrar desse produto notável um pouco modificado aqui:

Retomando dessa expressão temos que:

Então:

E que

Só que :

Então , precisamos somar então e dentro da expressão:

Então ajeitando a expressão de dentro temos que:

Voltando para a integral, ela fica assim:

Paramos nessa expressão da integral

Essa função é uma parte de uma circunferência de centro e raio igual a .

O gráfico é assim:

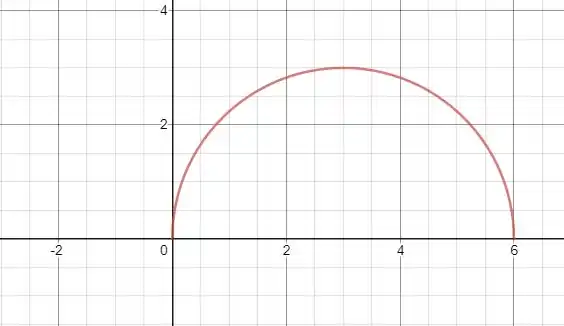
Essa figura é metade de uma circunferência de raio , então a sua área é dada por ,Então:

Já que a integral é numericamente igual a área, podemos afirmar que