Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 48
Esboce a região delimitada pela curva fornecida e calcule sua área:
,
Passo 1
E aí, galerinha!
Nesse problema temos que esboçar a região e calcular a área delimitada pela curva:
E pela reta:
Tem ideia de como fazemos isso?
Primeiro vamos esboçar a curva e as retas para determinar a região.
E para calcular a área, podemos calcular a integral da curva e a partir das retas, definir os limites de integração.
Veja só!
Passo 2
A curva pode ser reescrita como
Então pela estrutura da equação, temos uma parábola voltada para baixo, com o vértice transladado unidade para a direita e unidade para cima, ou seja:
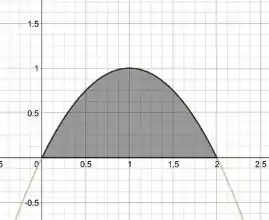
Pela região, podemos definir a área como a integral de com entre .
Em forma de integral essa área é:
Tranquilo até aqui?
Passo 3
Para resolver essa integral vamos aplicar a parte 2 do TFC.
Onde é a função primitiva de , ou seja, .
Precisamos encontrar a função primitiva de
Pra isso vamos lembrar da regrinha inversa da derivada da potência:
Ou seja:
Com a primitiva de em mãos, podemos aplicar o TFC.
Portanto, a área da região é dada por:
E aí! entendeu tudo? Responde Aí!