Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 15
Esboce a região delimitada pelas curvas fornecidas e encontre sua área.
Passo 1
Eaeee, belezinha?? Bom.. a questão nos pede para esboçar a região delimitada pelas seguintes curvas no intervalo :
E
Para isso, devemos calcular os pontos de interseção entre as duas curvas.
A questão também nos pede para calcular a área.
Em outras palavras, iremos utilizar a seguinte definição de área :
Onde essa área é representada na seguinte figura:
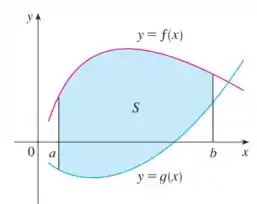
Dessa forma, devemos encontrar primeiro a interseção das curvas para prosseguirmos com o cálculo da área .
E aí?? Bora lá?? 😉
Passo 2
Para esboçarmos a região delimitada pelas curvas vamos esboçar ambas as curvas em um mesmo gráfico e, assim, vamos obter
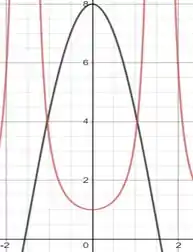
Resta-nos saber onde é que essas curvas vão se interceptar e para isso vamos igualar suas equações fazendo
Para o intervalo dado vamos ter como solução , ou seja:
Passo 3
Agora, para encontrarmos a área da região delimitada pelas curvas precisamos calcular a integral da função que está por cima menos a função que está por baixo e os limites de integração serão dados pelos valores de do intercepto das curvas. Então, teremos
Resposta
