Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 32

Esboce a região delimitada pelas curvas fornecidas e indique sua área

y = ln ⁡ x x ,     y = ln ⁡ x 2 x

Passo 1

Esboçando a região delimitada pelas curvas teremos o seguinte

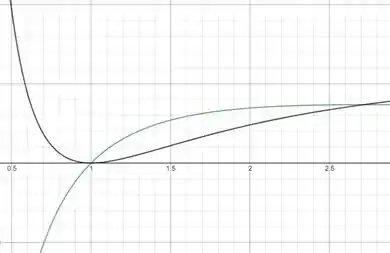
Para encontrarmos os limites de integração vamos igualar as duas equações e teremos

ln ⁡ x x = ln ⁡ x 2 x → ln ⁡ x = ln ⁡ x 2 → ln ⁡ x - ln ⁡ x 2 = 0

ln ⁡ x ⋅ 1 - ln ⁡ x = 0 → ln ⁡ x = 0 → x = 0

o u   1 - ln ⁡ x = 0 → x = e

Por fim, integraremos de 1 a e a função de cima menos a função de baixo

∫ 1 e ln ⁡ x x - ln ⁡ x 2 x d x = ln 2 ⁡ x 2 - ln 3 ⁡ x 3 1 e =

ln 2 ⁡ e 2 - ln 3 ⁡ e 3 = 1 2 - 1 3 = 1 6 u . a

Resposta

1 6 u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular a área da região limitada pelas seguintes curvas, dadas na forma paramétrica. x = t y = t 2 e x = 1 + t y = 1 + 3 t
Calcular a área da região S, hachurada na Figura 8.12. x = k ( t - s e nt ) y = k ( 1 - cos ⁡ t )
Calcular a área delimitada pela hipociclóide{[[x = 4 sen^3 t],[y = 4 cos^3 t]])
Calcular a área da região delimitada pela elipse{[[x = 3 cos t],[y = s e n t]])
Calcular a área da região limitada à direita pela elipse x = 3 cos ⁡ t y = 2s e nt ,e à esquerda pela reta x = 3 3 2 .