Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 36
Use um gráfico para encontrar coordenadas aproximadas dos pontos de interseção das curvas fornecidas. Em seguida, use sua calculadora para encontrar (aproximadamente) o volume do sólido obtido girando sobre o eixo a região delimitada por essas curvas.
Passo 1
Seguindo as instruções do enunciado vamos plotar ambas as funções em um mesmo gráfico a fim de encontrarmos o ponto de interseção entre as curvas. Então, teremos
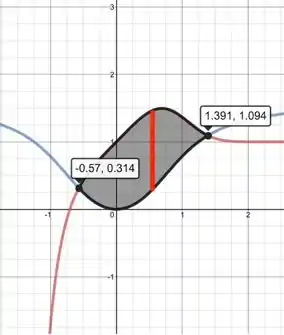
Quando rotacionarmos a curva obtida em torno do eixo vamos obter e . Assim, nosso volume será dado por
Utilizando uma calculadora obtemos a seguinte aproximação para a integral
Resposta
Exercícios de Livros Relacionados
Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que : y 2 ≤ 2 x - x 2 ,y ≥ 0
Calcule o volume do sólido cuja base é o semicírculo x 2 + y 2 ≤ r 2 , y ≥ 0 , e cujas seções perpendiculares ao eixo x são triângulo equiláteros:
2.Calcule o volume do sólido cuja base é o quadrado de vértices ( 0,0 ) , ( 1,1 ) , ( 0,1 )e( 1,0 ) e cujas seções perpendiculares ao eixo x são triângulos isósceles de altura x - x 2
2.Calcule o volume do sólido cuja base é o semicírculo 4 x 2 + y 2 ≤ 1 , y ≥ 0 , e cujas seções perpendiculares ao eixo x são semicírculos:
Ache o comprimento do arco da curva y = ln c o s s e cxd ex = π 6 ax = π 2 .