Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.4 - Ex. 40
Calcular a área entre o arco da hipociclóide
,
e a reta .
Passo 1
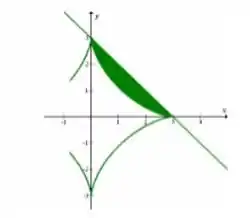
Primeiro devemos analisar a área do arco da hipociclóide:
Integrando:
Aplicando os limites, temos:
Passo 2
Agora devemos analisar a área da reta :
Integrando:
Aplicando os limites, temos:
Passo 3
Para finalizar subtraímos de , já que vem por cima como podemos ver no gráfico traçado.
Resposta
Exercícios de Livros Relacionados
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da
Dois carros de corrida, lado a lado em uma pista reta, movem-se com funções velocidade v 1 t m / s e v 2 m / s , respectivamente. Suponha que ambos estejam alinhados no instante t = 60s . Interprete o
Encontre a região englobada pela curva y = s e nx e a reta que passa pelos pontos ( 0,0 ) e 5 π 6 , 1 2 na curva.
Encontre uma reta vertical x = k que divida a área englobada pelas curvas x = y , x = 2 e y = 0 em duas partes iguais.
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da