Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.4 - Ex. 39

Calcular a área da região entre as curvas

{[[x = 4 cos t],[y = 2 s e n t]]) e {[[x = cos t],[y = s e n t]])

Passo 1

A = int_(t_0)^t y (t) * x ' ( t ) d t

x^' = - 4 s e n t

x^' = - s e n t

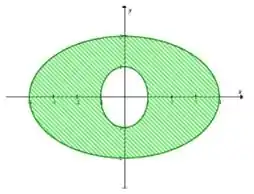
Primeiro devemos descobrir a área considerando a abertura interna:

A_1 = 4 int_((pi)/(2))^0 4 s e n t * (- 2 s e n t) d t = - 32 int_((pi)/(2))^0 s e n^2 t d t

Integrando:

A_1 = - 16 t + 8 s e n 2 t

Aplicando os limites, temos:

A_1 = - 16 (0 - (pi)/(2)) + 4 (s e n 0 - s e n pi) = 8 pi

Passo 2

Agora, devemos descobrir a área da abertura interna:

A_2 = 4 int_((pi)/(2))^0 s e n t * (- s e n t) d t = - 4 int_((pi)/(2))^0 s e n^2 t d t

Integrando:

A_2 = - 2 t + s e n 2 t

Aplicando os limites, temos:

A_2 = - 2 (0 - (pi)/(2)) + (s e n 0 - s e n pi) = pi

Passo 3

Para finalizar, subtraímos A_2 de A_1 :

A = A_1 - A_2 = 8 pi - pi = 7 pi

Resposta

7 pi u . c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Dê uma estimativa para o valor de k ( 0k1 ), tal que a região englobada por y = 1 / 1 - x 2 , y = x ,x = 0 e x = k tenha uma área de 1 unidade.
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. x = y 3 - y , x = 0
Encontre a área da região englobada pela parábola y = 2 x - x 2 e o eixo x .Encontre o valor de m de tal forma que a reta y = m x divida a região de (a) em duas regiões de mesma área.