Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.5 - Ex. 26
26. Dê um exemplo para mostrar que o centroide de uma região plana não é necessariamente um ponto dentro da região.
Passo 1
Vamos calcular o centroide dessa figura 1.
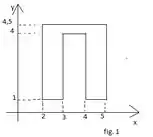
Primeiro dividimos a figura em figuras simples de calcular, logo há três figuras, sendo elas retângulos. Para calcular fazemos;
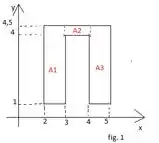
Passo 2
Passo 3
Centroide
Resposta
Centroide E como pode ser visto, não esta contido na figura
Exercícios de Livros Relacionados
Ache a taxa de variação da medida da área do Exercício 48 em relação a p quando p = 3 8 .
Ache a área da seção limitada pela curva y = tan 2 x , pelo eixo x e pela reta x = 1 4 π .
Ache a área da região limitada pelas três curvas y = x 2 ,y = 8 - x 2e4 x - y + 12 = 0 .
Ache a área da região limitada pela reta x = 4 e pela curva x 3 - x 2 + 2 x y - y 2 = 0 . (Sugestão: resolva a equação cúbica em y em termos de x e expresse y como duas funções de x.)
Ache a área da seção limitada pelas curvas y = sin x e y = cos x entre dois pontos de interseção consecutivos.