Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 27
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Para esse caso, primeiro vamos achar a interseção das duas primeiras equações, para depois achar onde ela é delimitada por .
Com isso, temos
O nosso gráfico fica assim:
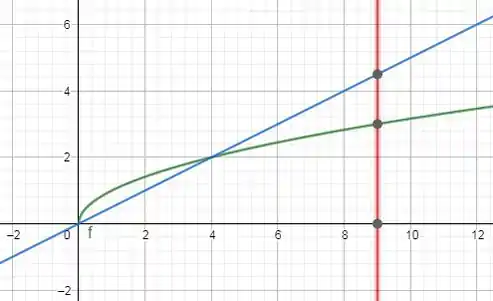
Então vamos integrar duas regiões: a primeira região vai de até ; e a segunda região vai de até
Passo 2
Organizando a integral, temos:
Resolvendo...
Então, isso resultará em:
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Suponha que a velocidade de uma formiga correndo ao longo da beirada de um muro seja modelada pela função v t =5 t , 0 ≤ t1 6 t - 1 t , 1 ≤ t ≤ 2 onde t está em segundos e v está em centímetros por se
Suponha que a função velocidade uma partícula em movimento retilíneo ao longo de um eixo s seja v t = 20 t 2 - 110 t + 120m / s e que a partícula esteja no instante t = 0 .Use um recurso gráfico para
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. Cada afirmação se refere a uma partícula em movimento retilíneo.Se a partícula tiver aceleração constante não nula, então o
Suponha que a velocidade de um camundongo correndo ao longo do rodapé de um quarto seja modelada pela função v t = 3 t 2 + 1 - 0,5 t,0 ≤ t ≤ 6 onde t está em segundos e v está em metros por segundo (m
Suponha que a função aceleração de uma partícula em movimento retilíneo ao longo de um eixo s seja a t = 4 t - 30m / s 2 e que a posição e a velocidade no instante t = 0 sejam s 0 = - 5 m e v 0 = 3m /