Suponha que a função velocidade uma partícula em movimento retilíneo ao longo de um eixo seja e que a partícula esteja no instante .
Use um recurso gráfico para gerar os gráficos de para os primeiros segundos de movimento.
Passo 1
E aí, tudo joia?
Bom, aqui a gente tem a velocidade. Pra descobrir a função a gente tem que integrar essa função:
No instante , a gente vai considerar a posição sendo também, então a nossa função é essa aí.
Passo 2
Já pra função de aceleração, a gente deriva a função da velocidade.
Show! Agora que a gente tem as três funções, vamos plotar os gráficos delas...
Passo 3
Aqui está:
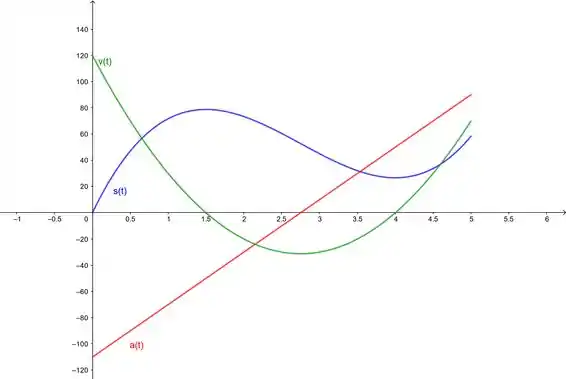
Prontinho!
Resposta
Gráfico