Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.7 - Ex. 22

Suponha que a função aceleração de uma partícula em movimento retilíneo ao longo de um eixo s seja a t = 4 t - 30   m / s 2 e que a posição e a velocidade no instante t = 0 sejam s 0 = - 5 m e v 0 = 3   m / s . Use um recurso gráfico para gerar os gráficos de s t ,   v t e   a ( t ) para os primeiros 25 segundos de movimento.

Passo 1

E aí, beleza?

Pra a gente fazer o gráfico precisa saber as funções. Vamos calcular então!

Nessa aqui a gente tem a aceleração, então a gente começa integrando pra achar a velocidade!

v t = ∫ 4 t - 30   d t

= 4 t 2 2 - 30 t + C

Esse C a gente mata com a informação que v 0 = 3 ...

v 0 = 4 0 2 2 - 30 0 + C = 3

C = 3

A função velocidade então é:

v t = 2 t 2 - 30 t + 3

Passo 2

Maravilha! Agora a gente integra essa da velocidade e acha a função da posição!

s t = ∫ 2 t 2 - 30 t + 3   d t

= 2 t 3 6 - 30 t 2 2 + 3 t + K

= t 3 3 - 15 t 2 + 3 t + K

E aí pra achar o K a gente joga a informação de que s 0 = - 5 :

s 0 = 0 3 6 - 15 0 2 + 3 0 + K =   - 5

K = - 5

Nossa função da posição então é:

s t =   t 3 3 - 15 t 2 + 3 t - 5

Passo 3

Ótimo! Agora só falta a gente plotar esses gráficos no intervalo [ 0,25 ] e voilà:

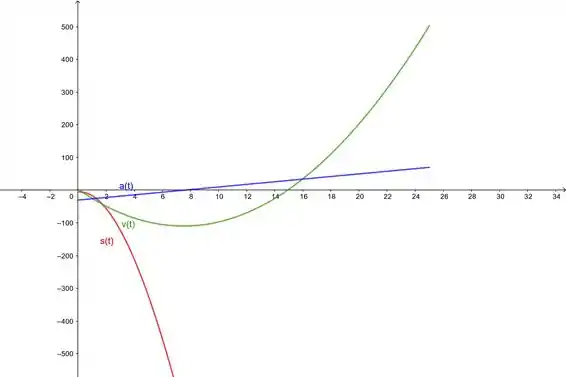
E prontinho!

Resposta

Gráfico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Dê uma estimativa para a área da região do primeiro quadrante englobada por y = s e n2 x e y = a r c s e nx .
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. y = 1 x 1 - ln ⁡ x 2 , y = 3 x
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. x = y 3 - 4 y 2 + 3 y , x = y 2 - y