Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 26

Esboce a região delimitada pelas curvas e visualmente estime a localização do centroide. Em seguida, calcule as coordenadas exatas do centroide

26. y = x ,   y = 0 ,   x = 4

Passo 1

O enunciado nos da as seguintes curvas:

y = x ,   y = 0 ,   x = 4

E pede pra a gente esboçar a região delimitada pelas curvas e estimar a localização do centroide, depois a gente deve calcular essas coordenadas!

Vamos começar esboçando:

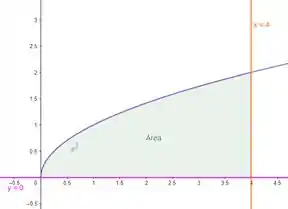
Agora vamos tentar adivinhar onde é o centroide hehe, vamos chutar mais ou menos x - = 2 e y - = 1 , mais ou menos aqui.

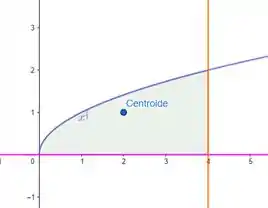
Passo 2

Agora vamos ver as coordenadas reais oficiais do nosso centroide, lembrando que as coordenadas do centroide são calculadas desse jeito aqui:

x - = 1 A ∫ a b x f x - g x d x

y - = 1 A ∫ a b 1 2 ( f x 2 - g x 2 ) d x

Como g x = 0 que seria y = 0 ficamos com:

x - = 1 A ∫ a b x f ( x ) d x

y - = 1 A ∫ a b 1 2 f x 2 d x

Passo 3

Antes de colocar a mão na massa para achar esses pontos vamos começar achando a área entre as funções. Como a nossa regição é delimitada pela função x e o eixo y = 0 entre x = 0 e x = 4 , ficamos com:

A = ∫ 0 4 x d x

A = 2 x 3 2 3   0 4

A = 2 × 3 3 2 3

A = 16 3

Passo 4

Show, agora vamos partir pra cima das nossas coordenadas. Começando por x :

x - = 1 16 3 ∫ 0 4 x x d x

Que é a mesma coisa que:

x - = 3 16 ∫ 0 4 x 3 2 d x

x - = 3 16 × 2 x 5 2 5   0 4

x - = 3 16 × 2 ( 4 ) 5 2 5   0 4

Resolvendo isso ai ficamos com:

x - = 3 16 × 2 5 × 32

x - = 12 5

Agora para y :

y - = 1 16 3 ∫ 0 4 1 2 ( x ) 2 d x

y - = 3 16 × 1 2 ∫ 0 4 x d x

y - = 3 32 × x 2 2 0 4

y - = 3 63 × 16

y - = 3 4

Uhul, achamos nosso centroide e até que chegamos perto do resultado :

x - , y - = 12 5 , 3 4

Resposta

x - , y - = 12 5 , 3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

26. O seguinte teorema é uma generalização do Teorema do valor médio para integrais: se f e g forem contínuas no intervalo fechado [ a , b ] e g x0 para todo x no intervalo aberto ( a , b ) , então ex
Suponha que f x0 e contínua em um intervalo [a,b]. Prove que ∫ a b f x d x0
Suponha f x0 e contínua em[a,b]. Prove que se ∫ a b f x d x = 0 , então f x = 0 , para todo x ∈ [ a , b ]
Se f x = x + 2 x - 3 , ache a média dos valores de f no intervalo 4,6 .
Se f x = 1 x , ache a média dos valores de f no intervalo 1,5 .