Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.3 - Ex. 2
Suponha e contínua em[a,b]. Prove que se , então , para todo
Passo 1
Como a nossa função é continua no intervalo [a,b] isso significa que a é limitada, isto é, existem valores máximos(M) e mínimos(m) em nossa função no intervalo [a,b], vamos chamar esses valores de e :
O enunciado diz pra gente que
Então nosso m é o valor mais próximo do valor mínimo que nossa função pode assumir que é 0, dessa forma:
Passo 2
Agora se integrarmos ambos os lados da equação obtemos:
Como temos uma integral definida e é uma constante, podemos falar que que é mesma coisa que: , então temos que
Dividindo ambos os lados por
Passo 3
Essa equação entre as desigualdades nada mais é que o teorema do valor médio, isto é, existe um ponto dentro da nossa curva entre o intervalo que representa uma altura e quando multiplicada pelo tamanho do nosso intervalo nos fornece um retângulo com área igual a da integral computada no intervalo .
Para explicar melhor isso, se liga nessa imagem aqui:
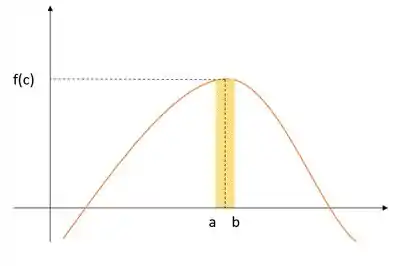
Agora da pra entender melhor, temos isso aqui:
Fazendo:
Obtemos:
Como é um comprimento e portanto um valor positivo, e nossa f(x) só pode assumir valores maiores ou igual a zero no intervalo [a,b], isso prova que:
Como f(c) é zero e f(x) não possui valores negativos no intervalo [a,b], para possibilitar áreas negativas como poderia ser o caso de uma senoide. Isso implica f(x) = 0
Resposta
em [a,b] se , pois nosso valor médio é zero quando a área abaixo da curva é zero no intervalo [a,b], forçando a condição de que o único valor possível que nossa função pode assumir dentro do intervalo [a,b] é 0 pois