Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 43

Esboce a região e encontre sua área (se for finita)

x , y ; x ≥ 1   ,   0 ≤ y ≤ 1 x 3 + x

Passo 1

Opa! Bora resolver esse problema. O enunciado diz que é pra a gente calcular a área da seguinte região:

  0 ≤ y ≤ 1 x 3 + x ,   x ≥ 1

Ou seja, a nossa região é delimitada pela curva 1 x 3 + x e pelo eixo y = 0 , além disso só vamos considerar valores maiores ou iguais a 1 para x . Desenhando isso em um gráfico:

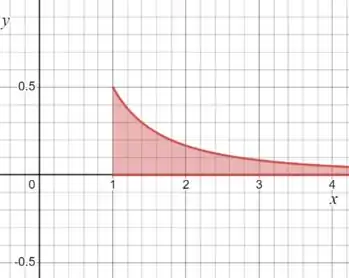
Repara que o que queremos é a área sobre a curva, então podemos escrever:

∫ 1 x 3 + x

Beleza, e os limites de integração?!

O x começa em 1 mas não tem um ponto final, então podemos escrever:

A =   ∫ 1 ∞   1 x 3 + x d x

O que temos em mãos é uma integral imprópria do tipo 1, a gente sabe disso pois um dos seus limites de integração é infinito.

Por definição temos que:

∫ a ∞ f ( x ) d x = lim t → ∞ ⁡ ∫ a t f ( x ) d x

Então temos que calcular:

lim t → ∞ ⁡ ∫ a t 1 x 3 + x d x

Passo 2

Agora vamos calcular a área:

A =     l i m t → ∞ ∫ 1 t   1 x ( x 2 + 1 ) d x

Podemos simplificar usando frações parciais:

1 x ( x 2 + 1 ) = A x + B x + C x 2 + 1 = A x 2 + A + B x 2 + C x x x 2 + 1

Cancelando o denominador:

A x 2 + A + B x 2 + C x = 1

Por igualdade de polinômios:

A = 1 C = 0 A + B = 0

B = - 1

Então temos:

A =     l i m t → ∞ ∫ 1 t   1 x - x x 2 + 1 d x

Passo 3

Vamos separar as integrais e calculalas:

  l i m t → ∞ ∫ 1 t   1 x   d x -   l i m t → ∞ ∫ 1 t   x x 2 + 1   d x  

    l i m t → ∞ ∫ 1 t   1 x   d x =   l i m t → ∞ ln ⁡ x 1 t

=   l i m t → ∞ ln ⁡ t - ln ⁡ 1 =   l i m t → ∞ ln ⁡ t

Agora a segunda:

l i m t → ∞ ∫ 1 t   x x 2 + 1   d x

Resolvendo a segunda integral, por substituição:

u = x 2 + 1     d u = 2 x   d x

Temos que :

∫ x x 2 + 1   d x = ∫ 1 2 u   d u = 1 2 ln ⁡ u + C

Voltabdo pra x e aplicando os limites de integração:

l i m t → ∞ ∫ 1 t   x x 2 + 1   d x =   l i m t → ∞ 1 2 ln ⁡ x 2 + 1 1 t

l i m t → ∞ 1 2 ln ⁡ x 2 + 1 1 t = l i m t → ∞ 1 2 ln ⁡ t 2 + 1 - 1 2 ln ⁡ 2

Lembrando que tínhamos:

A = l i m t → ∞ ∫ 1 t   1 x   d x -   l i m t → ∞ ∫ 1 t   x x 2 + 1   d x  

Portanto, juntando tudo:

A = l i m t → ∞ ln ⁡ t - l i m t → ∞ 1 2 + 1 2 ln ⁡ 2

Podemos reescrever:

A = l i m t → ∞ ln ⁡ t - 1 2 ln ⁡ t 2 + 1 + 1 2 ln ⁡ 2

Agora a gente vai usar as propriedades dos logaritmos:

ln ⁡ t - 1 2 ln ⁡ t 2 + 1 = ln ⁡ t - ln ⁡ t 2 + 1 1 2

= ln ⁡ t t 2 + 1

Além disso:

1 2 ln ⁡ 2 = ln ⁡ 2

Então podemos escrever:

A = l i m t → ∞ ln ⁡ t t 2 + 1 + ln ⁡ 2

Agora podemos calcular o limite:

l i m t → ∞ ln ⁡ t t 2 + 1 + ln ⁡ 2 = ln ⁡ 1 + ln ⁡ 2 = ln ⁡ 2

= ln ⁡ 2 = 1 2 ln ⁡ 2

Prontinho!!!

Resposta

A = 1 2 ln ⁡ 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se g x = sen 2 ⁡ x x 2 , use sua calculadora ou computador para fazer uma tabela de valores aproximados de ∫ 1 t g x d x para t = 2 , 5 , 10 , 100 , 1000 e 10000 . Parece que ∫ 1 ∞ g x d x é convergen
Se g x = 1 x - 1 , use sua calculadora ou computador para fazer uma tabela de valores aproximados de ∫ 2 t g x d x para t = 5 , 10 , 100 , 1000 e 10000 . Parece que ∫ 2 ∞ g x d x é convergente ou dive
Esboce a região e encontre sua área (se a área for finita). S = x ,y ; x ≥ 1 ,0 ≤ y ≤ e - x
Esboce a região e encontre sua área (se a área for finita). S = x ,y ; x ≥ 1 ,0 ≤ y ≤ 1 / ( x 3 + x )