Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 38
Esboce a região de integração e mude a ordem de integração.
Passo 1
E aii, pessoal?
A questão deu pra gente uma integral, e pediu pra gente desenhar a região de integração, e mudar a ordem (de para ).
Pelos limites de integração, a gente vê que essa região tá descrita como uma região do tipo I: com o entre dois valores constantes, e o entre duas funções de ...
Pra mudar a ordem de integração, a gente precisa transformar isso numa região do tipo II: com entre dois valores constantes, e entre duas funções de .
Passo 2
Essa região de integração tá definida assim:
Ou seja, está entre duas retas: e .
Como tá entre e , a região fica assim:
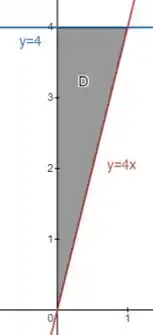
Passo 3
Pra mudar a ordem de integração, vamos agora enxergar a região como uma região do tipo II. Então, vamos reescrever a reta como:
Voltando para o esboço:
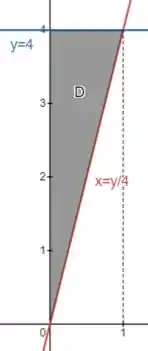
O tá variando de até essa reta , enquanto o varia de a :
Então a integral fica assim: