Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 49
Calcule a integral trocando a ordem de integração.
Passo 1
E aiii galera, tudo bem!? Bora começar!
A questão pede para calcular a integral abaixo trocando a ordem de integração.
Tá, beleza. Mas e agora?
Primeiro precisamos identificar qual o tipo de região que temos. Então, vamos lembrar da integral de região do tipo I e tipo II.
A região do tipo I é uma região limitada acima e abaixo por uma curva, e limitada lateralmente por retas verticais.
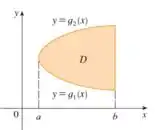
Já uma região do tipo II é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais.
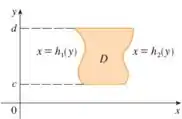
Conhecendo as regiões acima, e comparando com a integral dada, sabemos que nossa região é do tipo II. Nosso objetivo vai ser transforma-la na região tipo I, e depois calcula o valor da integral.
Devemos primeiro fazer o esboço da região, para compreender bem a inversão de ordem.
Vamos aos trabalhos!
Passo 2
O primeiro passo é esboçar a região.
Analisando nossa integral:
Sabemos que nosso domínio é:
Esboçando essas curvas, temos:
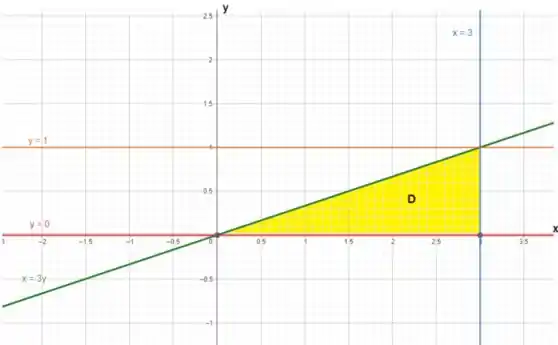
Observe que nossa região em amarelo, está contida no domínio mencionado acima.
Invertendo a ordem de integração, temos que os intervalos para o tipo I é:
Passo 3
Já sabemos a ordem de integração do tipo I:
Sabemos também que nossa integral tem essa cara:
Logo, podemos reescrever nossa integral do tipo II para o tipo I. Vai ficar assim:
Passo 4
Agora precisamos encontrar a resposta da integral:
Lembre que sempre começamos a integrar de dentro para fora.
Integrando em dy, temos:
Aplicando os limites de integração, temos:
Ficamos com uma integral simples em . Repare que precisamos fazer uma substituição do tipo:
Assim, ficamos com:
Integrando em relação a e voltando para a variável x, temos:
Aplicando os limites de integração:
Logo, a resposta da integral é: