Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 40
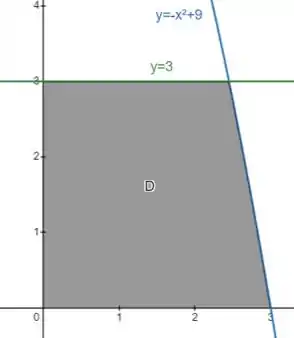
Esboce a região de integração e mude a ordem de integração.
Passo 1
Faala, belezinha??
Pra essa questão, precisamos que desenhar a região de integração dessa integral que eles deram, e depois mudar a ordem de integração.
A gente vai usar os limites de integração de e e desenhar a região de integração, que está descrita como uma região do tipo II: com entre dois valores constantes, e entre duas funções de .
Pra mudar a ordem de integração, a gente precisa transformar isso numa região do tipo I: com o entre dois valores constantes, e o entre duas funções de .
Passo 2
A região de integração é definida por:
O ta limitado pelo eixo () e pela curva:
Essa curva é uma parábola:
Só que além disso, temos que o está entre e :
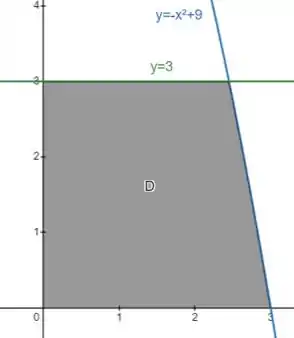
Passo 3
Não conseguimos escrever essa região como região do tipo I, porque o é limitado por cima por duas funções diferentes de : a reta até um ponto e depois a curva .
Então, pra mudar a ordem de integração vamos ter que dividir em duas regiões:
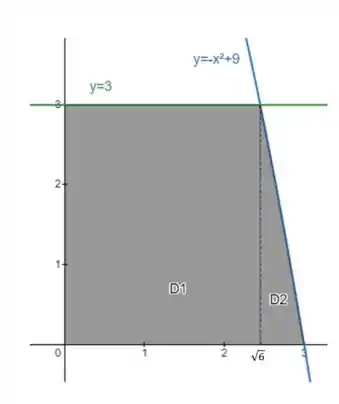
O ponto que divide as duas regiões é exatamente o valor de onde as curvas se interceptam:
Então:
Como estamos no primeiro quadrante ():
Agora vamos definir a nossa integral, que vai ficar dividida em duas:
Passo 4
Primeiro definindo o , que é uma região retangular:
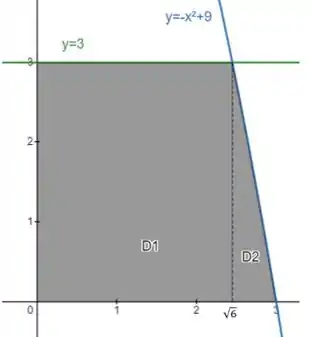
Então:
Por último, tem entre a curva e o eixo (), e varia de até , então
E:
Juntando as duas:
Resposta
