Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 39
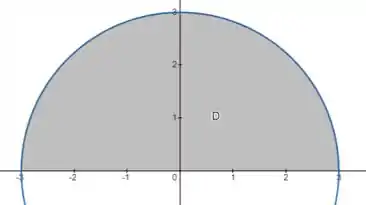
Esboce a região de integração e mude a ordem de integração.
Passo 1
Falaa, pessoal!
Nessa questão a gente precisa desenhar a região de integração dessa integral que ela deu, e depois trocar a ordem de integração (de para ).
Pra fazer isso, a gente primeiro vai olhar pros limites de integração de e pra conseguir definir a região, que é do tipo II:
Depois de desenhar, a gente vai precisar transformar em uma região do tipo I:
E ai sim conseguimos mudar a ordem de integração.
Passo 2
A região é definida assim:
Ou seja, o tá entre essas duas curvas:
Percebe que se a gente elevar essa expressão a quadrado, a gente chega da mesma expressão:
Isso é uma circunferência de raio , centrada na origem. Mas como estamos com entre e , a região é só metade do círculo:
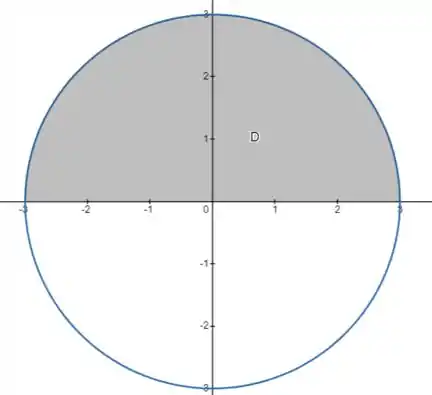
A curva é a metade direita da circunferência (), enquanto é a metade esquerda ().
Passo 3
Agora vamos mudar a ordem de integração!
Como queremos que esteja entre duas funções de , vamos voltar pra nossa expressão da circunferência, e isolar o :
A primeira expressão é a metade superior da circunferência (), enquanto a segunda é a parte inferior ().
Voltando pra nosso desenho:
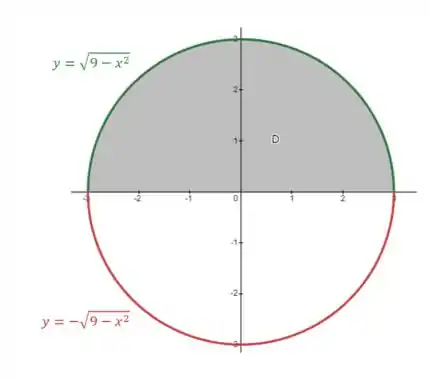
Como a região está entre a curva verde () e o eixo ():
E o tá variando de até :
Então a integral fica assim:
Resposta
