Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 37
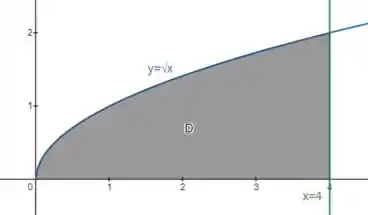
Esboce a região de integração e mude a ordem de integração.
Passo 1
Faala, galera!!
Nessa questão a gente precisa fazer duas coisas:
Primeiro, esboçar a região de integração dessa integral que ele deu.
Depois, mudar a ordem de integração (de para ).
Como que a gente faz isso?
Bom, pelos limites de integração a gente consegue saber que essa região está sendo expressa como uma região do tipo I:
Então pra esboçar a gente vai desenhar essas curvas e , e pegar a área entre elas no intervalo .
Pra mudar a ordem de integração, a gente vai olhar pra essa região e expressar ela como uma região do tipo II:
E ai conseguimos mudar a ordem de integração!
Vamos lá!
Passo 2
A região é definida assim:
Então seu esboço fica assim:
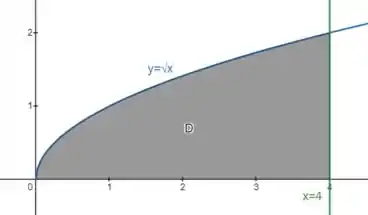
A curva é metade de uma parábola “deitada”, porque é equivalente à curva , mas com .
Passo 3
Pra mudar a ordem de integração, vamos voltar para o nosso esboço, mas agora olhando a curva como :
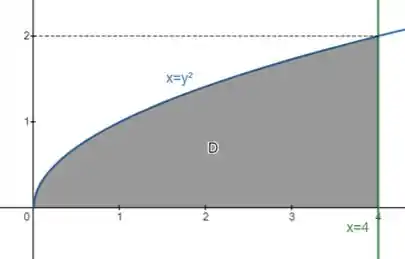
Percebe que essa região está entre e , e o está variando de até .
Então pra escrever como uma região do tipo II fica assim:
Ou seja, a integral fica:
Resposta
