Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 52
Calcule a integral trocando a ordem de integração.
52.
Passo 1
Fala, galera! Tudo show?
A questão pede pra calcular a integral trocando a ordem de integração, ou seja, em vez de resolver, no nosso caso, e depois , vamos resolver primeiro e depois . Belê?
Mas cuidado! Se a gente inverte a ordem, invertemos também os limites de integração, tá?
Mão na massa! 😉
Passo 2
O primeiro passo é observar que tipo de região estamos trabalhando.
De acordo com a região que está sendo calculada, temos essas informações:
Ou seja, como temos no eixo pontos bem definidos, temos uma região do Tipo I.
Assim, podemos esboçar a região:
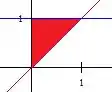
Onde a reta em vermelha é o limite em . Beleza?
Invertendo a ordem de integração, vamos ter que vai de até , enquanto varia de a .
Logo, teremos:
Passo 3
Agora resolvendo a integral dupla, faremos de dentro para fora, ou seja, primeiro em relação a .
Pela técnica da substituição, vamos chamar
Assim,
Podemos colocar esse para fora da integral como uma constante...
Resolvendo a integral...
Como sabemos quem é , substituímos junto com os limites de integração, tendo:
Agora integrando em relação a .
Colocando o termo em parêntesis para fora da integral, como se fosse uma constante...
Assim,