Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 47

Calcule a integral trocando a ordem de integração.

49.

∫ 0 1 ∫ a r c s e n   y π / 2 cos ⁡ x   1 + cos 2 ⁡ x   d x   d y

Passo 1

E aí, gente. Tudo beleza?

A questão quer o cálculo da integral, mas trocando a ordem de integração. Ou seja, nosso enunciado nos deu d x   d y , mas resolveremos primeiro d y e depois d x . Show, né?

O primeiro passo é esboçar a região de integração: enquanto y varia no intervalo [ 0,1 ] , x vai da curva x = a r c s e n   y (ou y = s e n   x ) até a reta x = π 2 .

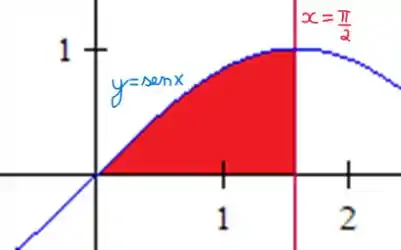
Mudando a ordem de integração, temos que y vai do eixo x até a curva y = s e n   x , com x no intervalo 0 , π 2 :

∫ 0 1 ∫ a r c s e n   y π 2 cos ⁡ x   1 + cos 2 ⁡ x   d x   d y

∫ 0 π 2 ∫ 0 s e n   x cos ⁡ x 1 + cos 2 ⁡ x   d y   d x

Passo 2

Fazendo de dentro para fora, a primeira integral em relação a y :

∫ 0 s e n   x cos ⁡ x 1 + cos 2 ⁡ x   d y

Só acrescentamos um y , já que não existia na função

y ⋅ cos ⁡ x ⋅ 1 + cos 2 ⁡ x 0 s e n x

s e n   x cos �� x   1 + cos 2 ⁡ x  

Agora integrando em relação a x , temos

∫ 0 π 2 s e n   x cos ⁡ x   1 + cos 2 ⁡ x   d x

Pela técnica da substituição, vamos chamar

u = 1 + cos 2 ⁡ x  

d u = - 2 cos ⁡ x   s e n   x   d x

d x = d u - 2 cos ⁡ x   s e n   x

Logo, substituindo

∫ 0 π 2 s e n   x cos ⁡ x   1 + cos 2 ⁡ x   d x

∫ 2 1   s e n   x cos ⁡ x ⋅ u   d u - 2 cos ⁡ x   s e n   x

∫ 1 2 u d u - 2

Jogando a fração pra fora da integral, como uma constante

1 2 ∫ 1 2 u   d u

1 3 u 3 1 2

Portanto,

1 3 ( 2 2 - 1 )

Resposta

∫ 0 1 ∫ a r c s e n   y π / 2 cos ⁡ x   1 + cos 2 ⁡ x   d x   d y = 1 3 ( 2 2 - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Inverta a ordem de integração.
Inverta a ordem de integração.
Inverta a ordem de integração.
Inverta a ordem de integração.
Inverta a ordem de integração.