Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 47
Esboce a região de integração e mude a ordem de integração.
Passo 1
Fala, galera! Tranquilo?
A questão pede para traçamos a região de integração de:
A região de integração de uma integral dupla é justamente de onde obtemos os limites de integração, então para encontrar essa região , nós vamos partir dos intervalos de derivação, que são:
E:
É possível observar que estamos trabalhando com uma região do tipo , pois os limites de integração de tem uma função, enquanto nos de só temos constantes. Para mudar a ordem de integração, vamos precisar expressar a região que vamos ter esboçado como uma região do tipo II.
Vem ver como fica!
Passo 2
A região de integração está entre o eixo e a curva , com . Agora que determinamos a nossa região, podemos esboça-la. Portanto:
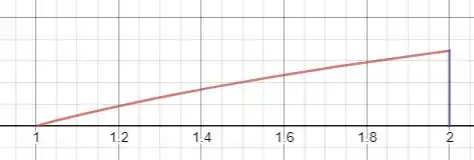
Devemos mudar a ordem de integração e reescrever a integral.
Passo 2
Vamos pensar que agora é uma região do tipo II, onde está entre dois valores constantes e está entre duas funções, que é o contrário da abordagem que fizemos no passo acima.
Temos que se:
Então, para deixarmos em função de podemos aplicar a exponencial dos dois lados da equação:
Como: , ficamos com:
Assim, mudando a ordem de integração, varia de até , enquanto vai de até .