Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 57
Calcule , onde é o disco , identificando primeiro a integral como o volume de um sólido.
Passo 1
Faala, pessoal!
Essa questão deu pra gente uma integral, e pede pra calcular, mas primeiro precisamos identificar de qual sólido que essa integral é volume!
Pra isso, a gente precisa lembrar que uma integral:
É o volume do sólido entre a superfície e o plano , sobre a região do plano .
Então o que a gente vai fazer é identificar a superfície , e a região , pra sabermos quem é esse sólido e calcular o volume!
Passo 2
A superfície que a gente quer descobrir é definida por essa expressão:
Percebemos primeiro que , então estamos acima do plano . Pra identificar essa superfície, vamos elevar os dois lados ao quadrado pra tirar essa raiz:
Essa superfície é uma esfera de raio centrada na origem:
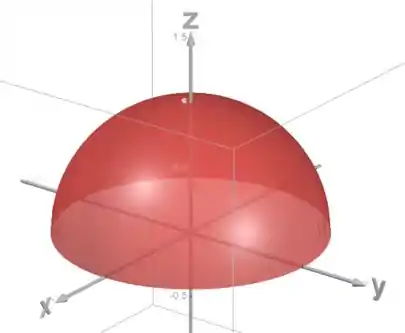
A região é definida por , então é um círculo de raio no plano centrado na origem.
Só que essa é exatamente a região embaixo da semiesfera que a gente achou agora!
Então o nosso sólido vai ser a região entre essa superfície e o plano :
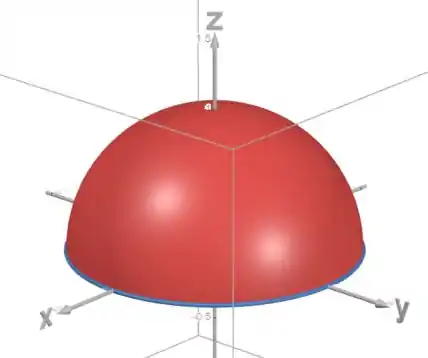
Essa curva em azul é o limite do disco .
Passo 3
Como já vimos, essa integral representa o volume do sólido que achamos no Passo 2:
O volume de uma esfera de raio é calculado por essa fórmula:
Como a nossa esfera tem raio :
E então:
E esse é o valor da integral!