Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.

17.

Esboçando as curvas vamos ter que a área entre elas é essa:

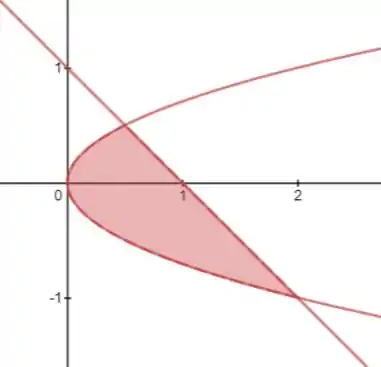
Para realizar a integração é melhor nós escrevermos a segunda função dessa forma:

Para essa área é melhor nós integrarmos em relação à , pois quando desenhamos o retângulo:

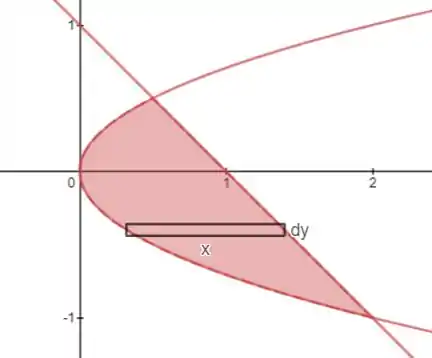
Aquele tamanho sempre pode ser escrito como a diferença entre a função e . Agora só precisamos descobrir quais são esses limites de integração, lembrando que precisamos da coordenada em . Para achar essas coordenadas só precisamos igualar as funções:

Resolvendo essa equação de segundo grau vamos obter esses dois valores para :

e

Então vamos fazer a nossa integração:

Fazendo as somas dentro da integral:

Essa é uma integral de polinômio que fica fácil de resolver, só somar um no expoente e dividir pelo expoente cada termo:

Aplicando os limites de integração:

Vamos tirar o mínimo multilplo comum e fazer a soma dessas frações: