Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 12
Esboce a região do plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas.
Passo 1
O problema pede para esboçar a região descrita por coordenadas polares. Nesse caso, temos
Vamos dividir o estudo em duas partes: primeiro para . Assim, temos
Portanto estamos dentro do círculo de raio . Como , isso representa a seguinte região:
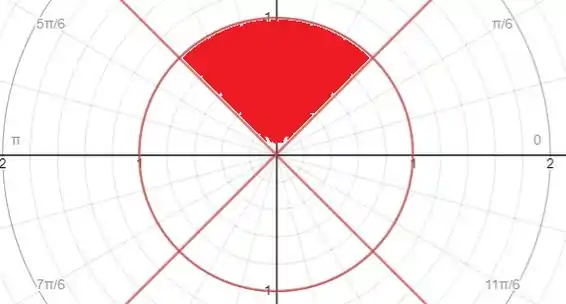
Passo 2
Agora vamos olhar para . Neste caso,
Isso também representa a região interna ao círculo de raio . Como , seríamos levados a pinta a mesma região do passo anterior. Porém, neste caso, como é negativo, temos que rebater para o quadrante oposto:
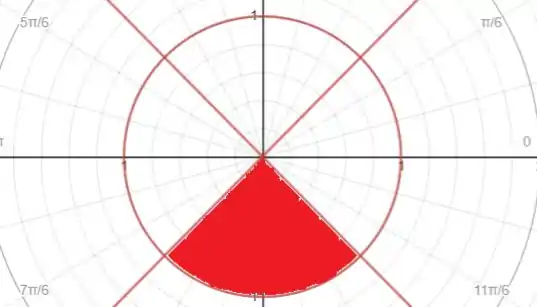
Passo 3
Juntando os dois casos:
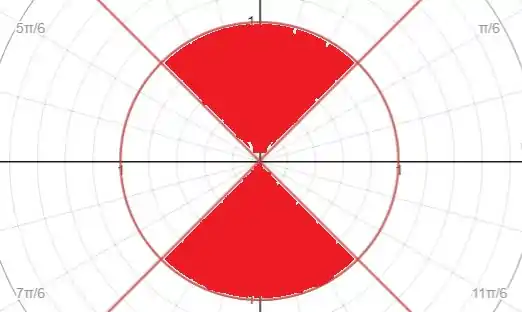
Resposta
Esboço.
Exercícios de Livros Relacionados
Um sólido é constituído do conjunto de pontos que está acima do cone z = x 2 + y 2 e abaixo da esfera x 2 + y 2 + z 2 = z . Descreva o sólido utilizando inequações envolvendo coordenadas esféricas.
Escreva a equação (a) em coordenadas cilíndricas e (b) em coordenadas esféricas. x = 3
Escreva a equação (a) em coordenadas cilíndricas e (b) em coordenadas esféricas. x 2 + y 2 + y 2 = 2
Identifique a superfície cuja equação é dada. ρ 2 ( sen 2 ϕ cos 2 θ + cos 2 ϕ ) = 4
Identifique a superfície cuja equação é dada. ρ = 2 cos ϕ