Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 49
Mostre que a curva polar (chamada conchóide) tem a reta como uma assíntota vertical mostrando que no limite . Use esse fato para ajudar a esboçar a conchóide.
Passo 1
O exercício fornece uma curva em coordenadas polares:
Que pode ser reescrita como:
É pedido para mostrarmos que a reta é uma assíntota vertical. Isso significa que nossa curva polar vai chegar bem perto da reta mas nunca irá toca-la.
Para isso, temos que mostrar que
Note que quando .
Assim, temos que tomar o limite de quando .
Passo 2
Como :
Quando
Assim,
Portanto, quando explode, .
Assim, a reta é assíntota vertical da curva. Um esboço dela é dado a seguir:
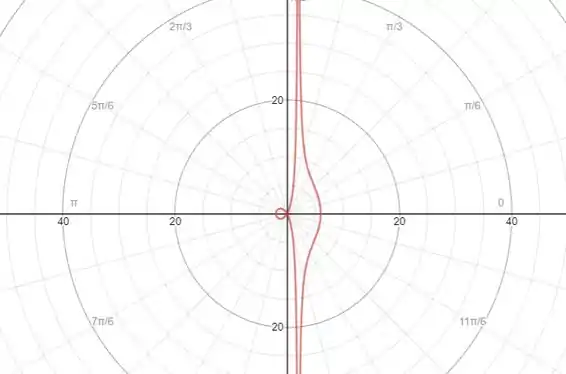
Resposta
Demonstração e esboço.
Exercícios de Livros Relacionados
Trace as curvas y = x 3 - 4 x e x = y 3 - 4 y e encontre seus pontos de intersecção, com precisão de uma casa decimal.
Trace a curva x = y - 3 y 3 + y 5
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de θ em coordenadas cartesianas. r = - 2 sen θ
18. Trace a cônica r = 4 / ( 5 + 6 cos θ ) e sua diretriz. Também trace a curva obtida pela rotação dessa cônica ao redor de seu foco por um ângulo π / 3 .
A ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumentaB ) Elimine os parâmetros para encontrar uma equação