Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.8 - Ex. 11
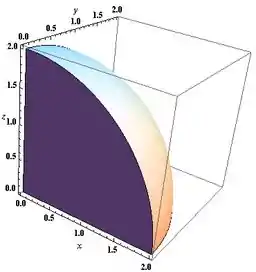
Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
Fala, gente boa! Tudo beleza?
A questão quer que a gente esboce o sólido que é descrito por:
Bom, como temos uma região em função de , o que temos aqui é uma região descrita em coordenadas esféricas.
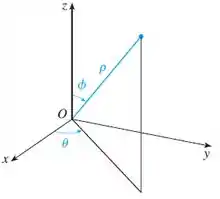
Esquema de representação de um ponto em coordenadas esféricas
Então, vamos analisar variável por variável, achar o comportamento de cada uma e entender qual sólido cada uma dessas variações vão formar.
Vamos lá!
Passo 2
Vamos entender a variação de cada variável no espaço.
- : Como essa variável é uma distância radial da origem e nós temos que:
- : Como vemos na imagem do passo , é um ângulo medido a partir do eixo . No nosso caso, temos:
- :
Como 2 é o valor máximo de e parte da origem, pode dizer que essa variável está representando uma circunferência no plano de raio .
Nosso percorre só Então nosso parte do eixo e para no plano . Isso quer dizer que teremos somente a metade positiva do nosso sólido em relação ao eixo .
Ou seja, no plano temos uma circunferência de raio , porém obedecendo a variação de , teremos só de círculo.
Passo 3
Usando a descrição que achamos, temos nosso sólido.
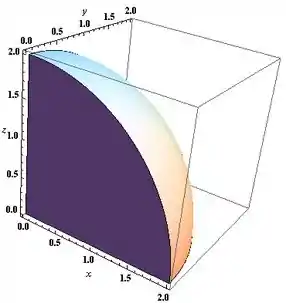
de uma meia esfera
Resposta
