Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.1 - Ex. 18
Use o resultado do Exercício para mostrar que
onde .
Passo 1
Fala, pessoal, beleza?
Essa questão pede pra gente provar uma inequação que ela da, usando o que achamos no exercício , que foi isso aqui:
O que a gente vai fazer é pegar essa função de dentro da integral, e encontrar dois limites pra ela, e escrever dessa forma:
Ai a gente vai integrar as três partes da inequação e usar o resultado do exercício .
Então vamos lá!
Passo 2
Vamos começar olhando pro domínio da função:
Desse domínio, temos que:
Esses são os argumentos de cosseno e seno dentro da nossa função (). Vamos pro círculo trigonométrico pra enxergar os valores de seno e cosseno nesse intervalo.
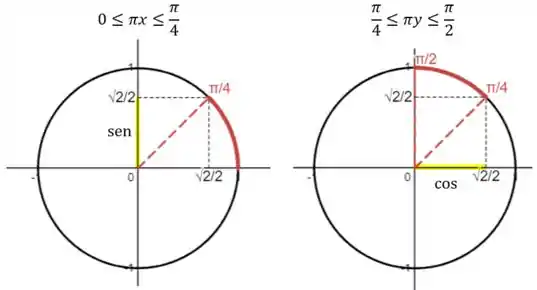
Percebe que pelo círculo trigonométrico, a gente vê que nesses intervalos temos:
E
Agora vamos lá... você concorda que se eu multiplicar esses dois termos o menor valor possível vai ser o produto do menor possível de cada, e o maior vai ser o produto dos maiores? Então fica assim:
Passo 3
Vamos então calcular a integral dos três termos da inequação:
A gente vai aplicar o resultado do exercício nas integrais da direita e da esquerda. Lembrando que é isso aqui:
No nosso caso, como , .
Então:
Então provamos que:
Resposta
Demonstrado na resolução