Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.10 - Ex. 31
Uma escada com de comprimento está apoiada contra uma parede vertical. Se a base da escada desliza afastando-se da parede a uma velocidade de , quão rápido está variando o ângulo entre o topo da escada e a parede quando o ângulo é ?
Passo 1
Opa, bora lá! Vamos analisar o que nosso probleminha está falando.
Bom, ele nos diz que uma escada de altura está apoiada numa parede, mas que sua base está escorregando a uma velocidade constante de , e nos pede a velocidade que o ângulo diminui cada vez que a escada cai, sabendo que ela já está com ângulo igual a .
Tem ideia de como fazemos isso?
Nesse problema temos que relacionar o ângulo que a escada varia com relação a horizontal com a velocidade da base da escada.
Pra isso podemos desenvolver uma função que nos dê o ângulo em função da distância horizontal que a base da escada está da parede. Assim, derivando com relação a podemos substituir os valores do enunciado e resolver o problema.
Veja só!
Passo 2
Primeiro vamos desenhar o problema para podemos visualizar o que estamos fazendo...
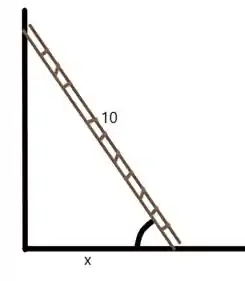
Nosso primeiro passo vai ser achar a relação com o ângulo:
Perceba que podemos relacionar o valor de com o ângulo pela lei do seno...
Assim, e são funções que variam com o tempo pois a escada está escorregando.
Então para encontrar a taxa de variação de ambos com relação ao tempo derivamos em
Como vimos anteriormente, é uma função de , então para calcular a derivada de temos que aplicar a regra da cadeia.
Substituindo na equação
Estamos interessados na variação de , então vamos isolá-lo em um lado da igualdade
Tranquilo até aqui?
Passo 3
Por fim, temos que substituir os valores dados no enunciado para descobrir a variação do ângulo .
Foi dado que e queremos saber a variação de quando .
Substituindo em
É isso! Entendeu tudo? Responde Aí!